题目内容
若a∈[2,6],b∈[0,4],
(1)求关于x的一元二次方程x2-2ax+b2=0有实数根的概率;
(2)求关于x的一元二次方程x2-2(a-2)x-b2+16=0没有实根的概率.
(1)求关于x的一元二次方程x2-2ax+b2=0有实数根的概率;
(2)求关于x的一元二次方程x2-2(a-2)x-b2+16=0没有实根的概率.
考点:几何概型
专题:概率与统计
分析:(1)求出方程x2-2ax+b2=0有实数根的等价条件,利用几何概型的概率公式,即可得到结论.
(2)作出不等式组对应的平面区域,利用几何概型的概率公式求出相应的面积即可得到结论.
(2)作出不等式组对应的平面区域,利用几何概型的概率公式求出相应的面积即可得到结论.
解答:
解:(1)若一元二次方程x2-2ax+b2=0有实数根,则△=4a2-4b2≥0,即a2≥b2,∴a≥b,
作出对应的平面区域如图1:
则E(2,2),F(4,4),B(6,4),C(6,0),D(2,0),A(2,4),
对应正方形ABCD的面积S=4×4=16,
五边形BCDEF的面积S=16-
×2×2=14,
则方程x2-2ax+b2=0有实数根的概率P=
=
=
.
(2)若关于x的一元二次方程x2-2(a-2)x-b2+16=0,则△=4(a-2)2-4(16-b2)<0,即(a-2)2+b2<16,
作出不等式组对应的平面区域如图2:
则扇形ADC的面积S=
×π×42=4π
则由几何概型的概率公式可得方程x2-2(a-2)x-b2+16=0没有实根概率P=
=
.
作出对应的平面区域如图1:
则E(2,2),F(4,4),B(6,4),C(6,0),D(2,0),A(2,4),
对应正方形ABCD的面积S=4×4=16,
五边形BCDEF的面积S=16-
| 1 |
| 2 |
则方程x2-2ax+b2=0有实数根的概率P=
| SBCDEF |
| SABCD |
| 14 |
| 16 |
| 7 |
| 8 |

(2)若关于x的一元二次方程x2-2(a-2)x-b2+16=0,则△=4(a-2)2-4(16-b2)<0,即(a-2)2+b2<16,
作出不等式组对应的平面区域如图2:

则扇形ADC的面积S=
| 1 |
| 4 |
则由几何概型的概率公式可得方程x2-2(a-2)x-b2+16=0没有实根概率P=
| 4π |
| 16 |
| π |
| 4 |
点评:本题主要考查概率的计算,根据几何概型的概率公式是解决本题的关键,注意利用数形结合进行求解..

练习册系列答案
相关题目
 爸爸和亮亮用4张扑克牌(方块2,黑桃4,黑桃5,梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,爸爸先抽,亮亮后抽,抽出的牌不放回.
爸爸和亮亮用4张扑克牌(方块2,黑桃4,黑桃5,梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,爸爸先抽,亮亮后抽,抽出的牌不放回.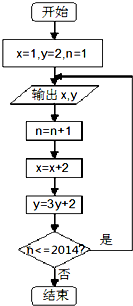 根据如图所示的程序框图,将输出的x值依次记为x1,x2,x3,…,x2014;输出的y值依次记为y1,y2,y3,…,y2014
根据如图所示的程序框图,将输出的x值依次记为x1,x2,x3,…,x2014;输出的y值依次记为y1,y2,y3,…,y2014