题目内容
已知:公差大于零的等差数列{an}的前n项和为Sn,且满足a3a4=117,a2+a5=22.求数列{an}的通项公式.
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:根据题意,由a3+a4=a2+a5,a3•a4的值求出a3、a4;由此求出
;即得通项公式an.
|
解答:
解:在等差数列{an}中,a3+a4=a2+a5=22,a3•a4=117,
∴a3,a4是方程x2-22x+117=0的两实根,
∵公差d>0,∴a3<a4,
∴a3=9,a4=13;
即
,
解得
;
∴通项公式为an=1+4(n-1)=4n-3.
∴a3,a4是方程x2-22x+117=0的两实根,
∵公差d>0,∴a3<a4,
∴a3=9,a4=13;
即
|
解得
|
∴通项公式为an=1+4(n-1)=4n-3.
点评:本题考查了等差数列的通项公式以及基本性质的应用问题,解题时应结合一元二次方程根与系数关系,求出a3、a4的值,是关键,属于基础题.

练习册系列答案
相关题目
tan19°+tan41°+
tan19°tan41°的值为( )
| 3 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、-
|
 爸爸和亮亮用4张扑克牌(方块2,黑桃4,黑桃5,梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,爸爸先抽,亮亮后抽,抽出的牌不放回.
爸爸和亮亮用4张扑克牌(方块2,黑桃4,黑桃5,梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,爸爸先抽,亮亮后抽,抽出的牌不放回.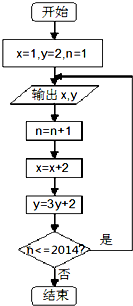 根据如图所示的程序框图,将输出的x值依次记为x1,x2,x3,…,x2014;输出的y值依次记为y1,y2,y3,…,y2014
根据如图所示的程序框图,将输出的x值依次记为x1,x2,x3,…,x2014;输出的y值依次记为y1,y2,y3,…,y2014