题目内容
在整数集Z中，被5除所得余数为k的所有整数组成一个“类”，记为[k]，则[k]=[5n+k]，k=0、1、2、3、4，则下列结论正确的是 ．
①2013∈[3]
②Z=[0]∪[1]∪[2]∪[3]∪[4]
③“整数a、b属于同一‘类’”的充要条件是“a-b∈[0]”
④命题“整数a、b满足a∈[1]，b∈[3]，则a+b∈[4]”的原命题与逆命题都为真命题．
①2013∈[3]
②Z=[0]∪[1]∪[2]∪[3]∪[4]
③“整数a、b属于同一‘类’”的充要条件是“a-b∈[0]”
④命题“整数a、b满足a∈[1]，b∈[3]，则a+b∈[4]”的原命题与逆命题都为真命题．
考点：整除的基本性质
专题：算法和程序框图
分析：利用“类”的意义和整数整除的意义即可得出．
解答：
解：①∵2013=402×5+3，∴2013∈[3]，正确；
②Z=[0]∪[1]∪[2]∪[3]∪[4]，正确；
③“整数a、b属于同一‘类’”?a=5m+k，b=5n+k，（m，n，k∈Z）?a-b=5（m-n）+0．
因此“整数a、b属于同一‘类’”的充要条件是“a-b∈[0]”，正确．
④命题“整数a、b满足a∈[1]，b∈[3]，则a+b∈[4]”的原命题为真命题；
若整数a、b满足a+b∈[4]，则整数可能a、b满足a∈[2]，b∈[2]”
因此其逆命题是假命题，故不正确．
故答案为：①②③．
②Z=[0]∪[1]∪[2]∪[3]∪[4]，正确；
③“整数a、b属于同一‘类’”?a=5m+k，b=5n+k，（m，n，k∈Z）?a-b=5（m-n）+0．
因此“整数a、b属于同一‘类’”的充要条件是“a-b∈[0]”，正确．
④命题“整数a、b满足a∈[1]，b∈[3]，则a+b∈[4]”的原命题为真命题；
若整数a、b满足a+b∈[4]，则整数可能a、b满足a∈[2]，b∈[2]”
因此其逆命题是假命题，故不正确．
故答案为：①②③．
点评：本题考查了“类”的意义和整数整除的意义，属于中档题．
练习册系列答案
相关题目
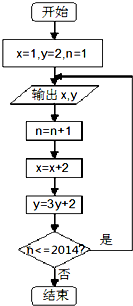根据如图所示的程序框图，将输出的x值依次记为x1，x2，x3，…，x2014；输出的y值依次记为y1，y2，y3，…，y2014设α，β都是锐角，且sinα=
，sinβ=
，则α+β=（ ）
| ||
| 10 |
| ||
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|