题目内容
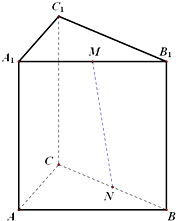 已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.
已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.(Ⅰ)证明:MN∥平面ACC1A1;
(Ⅱ)试求线段MN与平面ABC所成角的余弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(空间向量)依条件可知AB,AC,AA1两两垂直.以点A为原点,建立空间直角坐标系A-xyz.求出相关点的坐标,
(Ⅰ)利用
•
=0,得到
⊥
.通过
是平面ACC1A1的一个法向量,推出MN∥平面ACC1A1.
(Ⅱ)求出平面ABC的法向量是
=(x,y,z),利用法向量与向量
=(-
,0,-2)的夹角,求解所求线面所成角的余弦值.
(逻辑推理)(Ⅰ)作出AC的中点D,连结DN,A1D.通过证明四边形A1DNM是平行四边形,得到MN∥A1D,利用直线与平面平行的判定定理证明MN∥平面ACC1A1.
(Ⅱ)作出AB的中点F说明∠MNF就是所求的线面所成角,解三角形即可.
(Ⅰ)利用
| MN |
| AB |
| MN |
| AB |
| AB |
(Ⅱ)求出平面ABC的法向量是
| n |
| MN |
| 1 |
| 2 |
(逻辑推理)(Ⅰ)作出AC的中点D,连结DN,A1D.通过证明四边形A1DNM是平行四边形,得到MN∥A1D,利用直线与平面平行的判定定理证明MN∥平面ACC1A1.
(Ⅱ)作出AB的中点F说明∠MNF就是所求的线面所成角,解三角形即可.
解答:
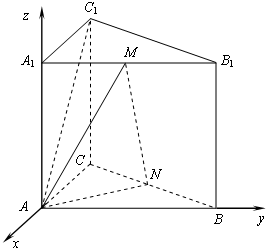 解:(空间向量)依条件可知AB,AC,AA1两两垂直.如图,
解:(空间向量)依条件可知AB,AC,AA1两两垂直.如图,
以点A为原点,建立空间直角坐标系A-xyz.
依条件可知AB,AC,AA1两两垂直.
如图,以点A为原点,建立空间直角坐标系A-xyz.
根据条件容易求出如下各点坐标:A(0,0,0),B(0,2,0),C(-1,0,0),A1(0,0,2),B1(0,2,2),C1(-1,0,2),M(0,1,2),N(-
,1,0).
(Ⅰ)因为
=(0,2,0),
=(-1,0,2),
因为
=(-
,0,-2),
=(0,2,0),所以
•
=-
×0+0×2-2×0=0,
从而
⊥
.
又因为
=(0,2,0)是平面ACC1A1的一个法向量,且MN?平面ACC1A1,
所以MN∥平面ACC1A1.
(Ⅱ)
=(-1,-2,0),
=(0,2,0)设平面ABC的法向量是
=(x,y,z)
由
•
=0,
•
=0,知法向量可以是
=(0,0,1),它与向量
=(-
,0,-2)的夹角满足:cosθ=
=-
,
所以所求线面所成角的余弦值是
.
(逻辑推理)(Ⅰ)如图
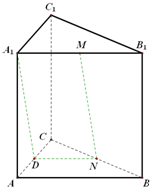
作出AC的中点D,连结DN,A1D.
∵D,N分别是AC,BC的中点
∴DN∥AB且DN=
AB,
∵ABC-A1B1C1是三棱柱,
∴AB∥A1B1且AB=A1BA
又∵M是A1B1的中点,
∴A1M=
A1B1=
AB=DN,
∵DN∥AB,AB∥A1B1
∴DN∥A1M∴四边形A1DNM是平行四边形
∴MN∥A1D
∵MN?平面ACC1,A1A1D?平面ACC1A1
∴MN∥平面ACC1A1.
(Ⅱ)如图

作出AB的中点F∵N,F分别是BC,AB的中点∴NF∥AC,NF=
AC=
又∵M是A1B1的中点,
∴MF∥AA1,MF=AA1=2
∵三棱柱ABC-A1B1C1的侧棱垂直于底面,
∴MF⊥面ABC,MF⊥NF
∴∠MNF就是所求的线面所成角.
∴cosMEN=
=
=
 解:(空间向量)依条件可知AB,AC,AA1两两垂直.如图,
解:(空间向量)依条件可知AB,AC,AA1两两垂直.如图,以点A为原点,建立空间直角坐标系A-xyz.
依条件可知AB,AC,AA1两两垂直.
如图,以点A为原点,建立空间直角坐标系A-xyz.
根据条件容易求出如下各点坐标:A(0,0,0),B(0,2,0),C(-1,0,0),A1(0,0,2),B1(0,2,2),C1(-1,0,2),M(0,1,2),N(-
| 1 |
| 2 |
(Ⅰ)因为
| AB |
| AC1 |
因为
| MN |
| 1 |
| 2 |
| AB |
| MN |
| AB |
| 1 |
| 2 |
从而
| MN |
| AB |
又因为
| AB |
所以MN∥平面ACC1A1.
(Ⅱ)
| BC |
| AB |
| n |
由
| n |
| BC |
| n |
| AB |
| n |
| MN |
| 1 |
| 2 |
| ||||
|
|
| 4 | ||
|
所以所求线面所成角的余弦值是
| 1 | ||
|
(逻辑推理)(Ⅰ)如图

作出AC的中点D,连结DN,A1D.
∵D,N分别是AC,BC的中点
∴DN∥AB且DN=
| 1 |
| 2 |
∵ABC-A1B1C1是三棱柱,
∴AB∥A1B1且AB=A1BA
又∵M是A1B1的中点,
∴A1M=
| 1 |
| 2 |
| 1 |
| 2 |
∵DN∥AB,AB∥A1B1
∴DN∥A1M∴四边形A1DNM是平行四边形
∴MN∥A1D
∵MN?平面ACC1,A1A1D?平面ACC1A1
∴MN∥平面ACC1A1.
(Ⅱ)如图

作出AB的中点F∵N,F分别是BC,AB的中点∴NF∥AC,NF=
| 1 |
| 2 |
| 1 |
| 2 |
又∵M是A1B1的中点,
∴MF∥AA1,MF=AA1=2
∵三棱柱ABC-A1B1C1的侧棱垂直于底面,
∴MF⊥面ABC,MF⊥NF
∴∠MNF就是所求的线面所成角.
∴cosMEN=
| NF |
| MN |
| ||||
|
| 1 | ||
|
点评:本题用两种方法证明直线与平面平行,直线与平面所成角的求法,考查空间想象能力以及计算能力,转化思想的应用.

练习册系列答案
相关题目
(文科)已知实数x,y满足
,则x2+y2的最小值为( )
|
A、
| ||||
B、
| ||||
| C、4 | ||||
| D、5 |
 如图,四棱锥E-ABCD,已知四边形ABCD为菱形,△AEC所在的平面垂直于平面ABCD,且∠EAC=∠BAD=60°,AD=2
如图,四棱锥E-ABCD,已知四边形ABCD为菱形,△AEC所在的平面垂直于平面ABCD,且∠EAC=∠BAD=60°,AD=2 圆台的上、下底面半径分别是10cm、20cm,它的侧面展开图--扇环的圆心角为180°,那么圆台的表面积是多少?(结果中保留π)
圆台的上、下底面半径分别是10cm、20cm,它的侧面展开图--扇环的圆心角为180°,那么圆台的表面积是多少?(结果中保留π)