题目内容
（文科）已知实数x，y满足
，则x2+y2的最小值为（ ）
|
A、
| ||||
B、
| ||||
| C、4 | ||||
| D、5 |
考点：简单线性规划
专题：计算题,作图题,不等式的解法及应用
分析：由题意作出其平面区域，x2+y2的几何意义是原点到阴影部分内的点的距离的平方，从而求解．
解答：
解：由题意作出其平面区域，
x2+y2的几何意义是原点到阴影部分内的点的距离的平方；
故原点到阴影部分内的点的距离的最小值为
原点到直线2x+y-4=0的距离，
d=
=
；
故x2+y2的最小值为
．
故选B．
x2+y2的几何意义是原点到阴影部分内的点的距离的平方；
故原点到阴影部分内的点的距离的最小值为
原点到直线2x+y-4=0的距离，
d=
| 4 | ||
|
4
| ||
| 5 |
故x2+y2的最小值为
| 16 |
| 5 |
故选B．
点评：本题考查了简单线性规划，作图要细致认真，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知P（x，y），A（3，1），B（1，2）在同一直线上，那么2x+4y的最小值是（ ）
A、2
| ||
B、4
| ||
| C、16 | ||
| D、20 |
当实数x、y满足
时，z=x+y既有最大值也有最小值，则实数a的取值范围是（ ）
|
A、(-∞， -
| ||||
B、(-
| ||||
C、(-∞， -
| ||||
D、(-
|
给出以下三个命题：
①在一元二次方程ax2+bx+c=0中，若b2-4ac≥0，则方程有实数根；
②若a＜b，则a-c＜b-c；
③若ab≥0，则a≥0或b≥0．
其中原命题、逆命题、否命题、逆否命题全都是真命题的是（ ）
①在一元二次方程ax2+bx+c=0中，若b2-4ac≥0，则方程有实数根；
②若a＜b，则a-c＜b-c；
③若ab≥0，则a≥0或b≥0．
其中原命题、逆命题、否命题、逆否命题全都是真命题的是（ ）
| A、①② | B、② | C、③ | D、②③ |
在△ABC中，a，b，c分别为内角A，B，C的对边，由所给的已知条件解三角形，其中有两解的是（ ）
| A、a=12，c=15，A=120° |
| B、a=30，c=28，B=60° |
| C、a=14，b=16，A=45° |
| D、b=20，A=120°，C=80° |
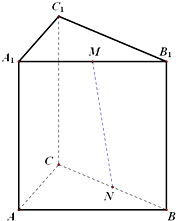已知三棱柱ABC-A1B1C1的侧棱垂直于底面，∠BAC=90°，AB=AA1=2，AC=1，M，N分别是A1B1，BC的中点．