题目内容
已知公差不为0的等差数列{an}的前n项和为Sn,S7=70,且a1,a2,a6成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=2n•an,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)设bn=2n•an,求数列{bn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用已知条件列出方程,求出数列的首项与公差,然后求数列{an}的通项公式;
(2)化简bn=2n•an,利用错位相减法,直接求数列{bn}的前n项和Tn.
(2)化简bn=2n•an,利用错位相减法,直接求数列{bn}的前n项和Tn.
解答:
解:(1)设公差为d(d≠0),由S7=70,且a1,a2,a6成等比数列得,7a1+21d=70,(a1+d)2=a1(a1+5d)(d≠0)
解得a1=1,d=3,∴an=3n-2….(6分)
(2)由(1),Tn=1×2+4×22+7×23+…+(3n-5)•2n-1+(3n-2)•2n∴2Tn=1×22+4×23+7×24+…+(3n-5)•2n+(3n-2)•2n+1
相减得,-Tn=2+3×22+3×23+…3•2n-(3n-2)•2n+1
=2+
-(3n-2)•2n+1
=(5-3n)•2n+1-10
∴Tn=(3n-5)•2n+1+10…(12分)
解得a1=1,d=3,∴an=3n-2….(6分)
(2)由(1),Tn=1×2+4×22+7×23+…+(3n-5)•2n-1+(3n-2)•2n∴2Tn=1×22+4×23+7×24+…+(3n-5)•2n+(3n-2)•2n+1
相减得,-Tn=2+3×22+3×23+…3•2n-(3n-2)•2n+1
=2+
| 12(1-2n-1) |
| 1-1 |
=(5-3n)•2n+1-10
∴Tn=(3n-5)•2n+1+10…(12分)
点评:本题考查干错事了的通项公式的求法,错位相减法的应用,考查数列求和方法的应用,基本知识与基本方法的考查.

练习册系列答案
相关题目
已知P(x,y),A(3,1),B(1,2)在同一直线上,那么2x+4y的最小值是( )
A、2
| ||
B、4
| ||
| C、16 | ||
| D、20 |
设f(x)是定义在R上的不恒为零的函数,且对于任意的a,b∈R满足f(ab)-af(b)=bf(a),f(3)=3,an=
,bn=
,n∈N*.有下列结论:
①f(
)=
;②f(x)为奇函数;③a2=-2;④b2=9.
其中正确的是( )
| f(3n) |
| 3n |
| f(3n) |
| n |
①f(
| 1 |
| 3 |
| 1 |
| 3 |
其中正确的是( )
| A、①②③ | B、③④ | C、①③ | D、②④ |
当实数x、y满足
时,z=x+y既有最大值也有最小值,则实数a的取值范围是( )
|
A、(-∞, -
| ||||
B、(-
| ||||
C、(-∞, -
| ||||
D、(-
|
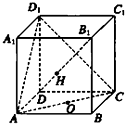 如图,在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,H为直线B1D与平面ACD1的交点,求证:D1、H、0三点共线.
如图,在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,H为直线B1D与平面ACD1的交点,求证:D1、H、0三点共线.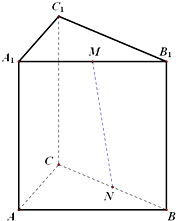 已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.
已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.