题目内容
已知函数y=f(x),x∈R,数列{an}的通项公式为an=f(n),n∈N*,那么“函数y=f(x)在[1,+∞)单调递增”,是“数列{an}为单调递增数列”的 条件.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据数列的函数性得出函数y=f(x)在[1,+∞)单调递增,数列{an}为单调递增数列,
反之:由“数列{an}为单调递增数列”,n是正整数,则不一定函数y=f(x)在[1,+∞)单调递增,可判断答案.
反之:由“数列{an}为单调递增数列”,n是正整数,则不一定函数y=f(x)在[1,+∞)单调递增,可判断答案.
解答:
解:函数y=f(x),x∈R,数列{an}的通项公式为an=f(n),n∈N*,
∵函数y=f(x)在[1,+∞)单调递增,
∴数列{an}为单调递增数列,
反之:由“数列{an}为单调递增数列”,∵n是正整数,
∴函数y=f(x)在[m,+∞)单调递增,m<1.5,
∴根据充分必要条件的定义可判断:
“函数y=f(x)在[1,+∞)单调递增”,是“数列{an}为单调递增数列”的充分不必要条件,
故答案为:充分不必要条件.
∵函数y=f(x)在[1,+∞)单调递增,
∴数列{an}为单调递增数列,
反之:由“数列{an}为单调递增数列”,∵n是正整数,
∴函数y=f(x)在[m,+∞)单调递增,m<1.5,
∴根据充分必要条件的定义可判断:
“函数y=f(x)在[1,+∞)单调递增”,是“数列{an}为单调递增数列”的充分不必要条件,
故答案为:充分不必要条件.
点评:本题考查数列的单调性,与函数的单调性的区别与联系,充分必要条件的定义,属于中档题,容易出错.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
给出以下三个命题:
①在一元二次方程ax2+bx+c=0中,若b2-4ac≥0,则方程有实数根;
②若a<b,则a-c<b-c;
③若ab≥0,则a≥0或b≥0.
其中原命题、逆命题、否命题、逆否命题全都是真命题的是( )
①在一元二次方程ax2+bx+c=0中,若b2-4ac≥0,则方程有实数根;
②若a<b,则a-c<b-c;
③若ab≥0,则a≥0或b≥0.
其中原命题、逆命题、否命题、逆否命题全都是真命题的是( )
| A、①② | B、② | C、③ | D、②③ |
已知函数f(x)是定义在[-5,5]上的偶函数,f(x)在[0,5]上是单调函数,且f (-3)<f ( 1 ),
则下列不等式中一定成立的是( )
则下列不等式中一定成立的是( )
| A、f (-1)<f (-3) |
| B、f (2)<f (3) |
| C、f (-3)<f (5) |
| D、f (0)>f (1) |
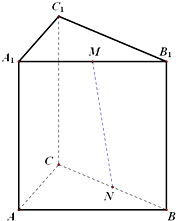 已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.
已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.