题目内容
 如图,四棱锥E-ABCD,已知四边形ABCD为菱形,△AEC所在的平面垂直于平面ABCD,且∠EAC=∠BAD=60°,AD=2
如图,四棱锥E-ABCD,已知四边形ABCD为菱形,△AEC所在的平面垂直于平面ABCD,且∠EAC=∠BAD=60°,AD=2| 3 |
| EG |
| GC |
| CD |
| CH |
(1)求证:EB⊥AD;
(2)求证:直线GH∥平面BEF.
考点:直线与平面平行的判定,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)只要证明BF⊥AD,AF⊥EF,利用线面垂直的判定得到AD⊥平面EFB,利用线面垂直的性质可证;
(2)证明:过D作DO∥GH,交EC与O,则O是EC 的中点,过O 作OM∥BC,交EB于M,连接MF,只要证明四边形DCMF是平行四边形,利用平行四边形的性质得到线线平行,再由线面平行的判定定理可得.
(2)证明:过D作DO∥GH,交EC与O,则O是EC 的中点,过O 作OM∥BC,交EB于M,连接MF,只要证明四边形DCMF是平行四边形,利用平行四边形的性质得到线线平行,再由线面平行的判定定理可得.
解答:
(1)证明:因为四边形ABCD为菱形,△AEC⊥平面ABCD,且∠EAC=∠BAD=60°,AD=2
,AE=4,F为AD的中点,
所以BF⊥AD,cos∠EAF=cos∠EAC.cos∠CAD=
×
=
,
所以EF2=AE2+AF2-2AE×AF×
=16+3-6=13,
所以AF2+EF2=AB2,
所以AF⊥EF,
所以AD⊥平面EFB,
所以AD⊥EB;
(2)证明:过D作DO∥GH,交EC与O,则O是EC 的中点,过O 作OM∥BC,交EB于M,连接MF,
则OM∥BC,OM=
BC=DF,
所以四边形DCMF是平行四边形,
所以OD∥MF,
所以GH∥MF,
又GH?平面BEF,MF?平面BEF,
所以GH∥平面BEF.
| 3 |
所以BF⊥AD,cos∠EAF=cos∠EAC.cos∠CAD=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
所以EF2=AE2+AF2-2AE×AF×
| ||
| 4 |
所以AF2+EF2=AB2,
所以AF⊥EF,
所以AD⊥平面EFB,
所以AD⊥EB;
(2)证明:过D作DO∥GH,交EC与O,则O是EC 的中点,过O 作OM∥BC,交EB于M,连接MF,
则OM∥BC,OM=
| 1 |
| 2 |
所以四边形DCMF是平行四边形,
所以OD∥MF,
所以GH∥MF,
又GH?平面BEF,MF?平面BEF,
所以GH∥平面BEF.
点评:本题考查了线面垂直的性质定理的运用以及线面平行的判定,关键是将所求转化为线线问题解决,属于难题

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
给出以下三个命题:
①在一元二次方程ax2+bx+c=0中,若b2-4ac≥0,则方程有实数根;
②若a<b,则a-c<b-c;
③若ab≥0,则a≥0或b≥0.
其中原命题、逆命题、否命题、逆否命题全都是真命题的是( )
①在一元二次方程ax2+bx+c=0中,若b2-4ac≥0,则方程有实数根;
②若a<b,则a-c<b-c;
③若ab≥0,则a≥0或b≥0.
其中原命题、逆命题、否命题、逆否命题全都是真命题的是( )
| A、①② | B、② | C、③ | D、②③ |
在△ABC中,a,b,c分别为内角A,B,C的对边,由所给的已知条件解三角形,其中有两解的是( )
| A、a=12,c=15,A=120° |
| B、a=30,c=28,B=60° |
| C、a=14,b=16,A=45° |
| D、b=20,A=120°,C=80° |
若点M(x,y)满足条件:
,则z=-x+y的取值范围是( )
|
| A、[-1,0] |
| B、[0,1] |
| C、[0,2] |
| D、[-1,2] |
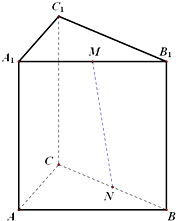 已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.
已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.