题目内容
已知过抛物线y2=2px(p>0)的焦点,斜率为2的直线l交抛物线于A、B两点,且|AB|=5.
(1)求此抛物线方程;
(2)若M(1,2)是抛物线上一点,求
•
的值.
(1)求此抛物线方程;
(2)若M(1,2)是抛物线上一点,求
| MA |
| MB |
考点:直线与圆锥曲线的关系,函数的零点,平面向量数量积的运算,抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)求出抛物线的焦点坐标,写出直线方程,与抛物线联立,利用弦长公式求出写出,即可求此抛物线方程;
(2)利用(1)消元后的方程,通过韦达定理,结合
•
的坐标表示即可求解数量积的值.
(2)利用(1)消元后的方程,通过韦达定理,结合
| MA |
| MB |
解答:
解:(1)因焦点F(
, 0),所以直线l的方程为y=2(x-
)
由
消去y得4x2-6px+p2=0①
设A(x1,y1),B(x2,y2),则x1+x2=
,
∴|AB| =x1+x2+p=
=5,∴p=2,
∴抛物线方程为y2=4x.(6分)
(2)方程①化为 x2-3x+1=0∴x1+x2=3,x1x2=1,
直线l的方程为y=2x-2,
∴
•
=(x1-1,y1-2)(x2-1,y2-2)
=(x1-1)(x2-1)+(y1-2)(y2-2)
=(x1-1)(x2-1)+(2x1-4)(2x2-4)
=5x1x2-9(x1+x2)+17
=5-27+17
=-5(12分)
| p |
| 2 |
| p |
| 2 |
由
|
设A(x1,y1),B(x2,y2),则x1+x2=
| 3p |
| 2 |
∴|AB| =x1+x2+p=
| 5p |
| 2 |
∴抛物线方程为y2=4x.(6分)
(2)方程①化为 x2-3x+1=0∴x1+x2=3,x1x2=1,
直线l的方程为y=2x-2,
∴
| MA |
| MB |
=(x1-1)(x2-1)+(y1-2)(y2-2)
=(x1-1)(x2-1)+(2x1-4)(2x2-4)
=5x1x2-9(x1+x2)+17
=5-27+17
=-5(12分)
点评:本题考查抛物线与直线方程的综合应用,写出公式的求法,向量的数量积的求法,考查转化思想以及计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
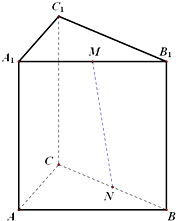 已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.
已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.