题目内容
在△ABC中,a,b,c分别是角A,B,C的对边,
(1)若a=
,b=
,B=45°,求角A,C和边c;
(2)若
=-
,b=
,a+c=4,求△ABC的面积.
(1)若a=
| 3 |
| 2 |
(2)若
| cosB |
| cosC |
| b |
| 2a+c |
| 13 |
考点:正弦定理,余弦定理
专题:计算题,解三角形
分析:(1)由正弦定理,求出sinA,再由A,运用三角形内角和定理,求出C,再运用正弦定理,求出c即可,注意两解;
(2)运用正弦定理和两角和的正弦公式,即可得到cosB,再由余弦定理,结合条件得到ac=3,由面积公式即可得到三角形ABC的面积.
(2)运用正弦定理和两角和的正弦公式,即可得到cosB,再由余弦定理,结合条件得到ac=3,由面积公式即可得到三角形ABC的面积.
解答:
解:(1)∵
=
∴sinA=
,
∴A=60°或120°,
∴当A=60°时,C=75°,c=2sinC=
;
当A=120°,C=15°,c=2sinC=
.
(2)∵
=-
∴2sinAcosB+cosBsinC=-sinBcosC
∴2sinAcosB+sin(B+C)=0,又sin(B+C)=sinA,
∴2cosB+1=0∴cosB=-
,∴-
=
,
∵a+c=4,b=
,
∴ac=(a+c)2-13=3,
∴△ABC的面积S=
acsinB=
×3×
=
.
| sinA | ||
|
| ||||
|
| ||
| 2 |
∴A=60°或120°,
∴当A=60°时,C=75°,c=2sinC=
| ||||
| 2 |
当A=120°,C=15°,c=2sinC=
| ||||
| 2 |
(2)∵
| cosB |
| cosC |
| sinB |
| 2sinA+sinC |
∴2sinAcosB+sin(B+C)=0,又sin(B+C)=sinA,
∴2cosB+1=0∴cosB=-
| 1 |
| 2 |
| 1 |
| 2 |
| a2+c2-b2 |
| 2ac |
∵a+c=4,b=
| 13 |
∴ac=(a+c)2-13=3,
∴△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
点评:本题考查正弦定理和余弦定理以及面积公式的运用,考查三角恒等变换公式的运用,考查化简运算能力,属于基础题.

练习册系列答案
相关题目
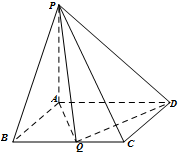 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=tBC(t>0)
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=tBC(t>0)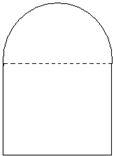 某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?
某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?