题目内容
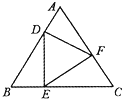 如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,且
如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,且| AD |
| DB |
| 1 |
| 2 |
考点:几何概型
专题:概率与统计
分析:由题意,本题属于几何概型,只要求出△DEF的面积与△ABC的面积比,就是所求概率.
解答:
解:如图,在△ABC内部随机取一点,则总的基本事件对应的区域为三角形ABC
要使该点取自△ABE内部,则所含的基本事件对应的区域为△DEF,
所以所求该点取自△DEF内部的概率就是两部分的面积比,
由已知等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,且
=
,则
=
,
∴△ADF,△BED,△CFE都是直角三角形,
∴
=
,
=
,
∴该点取自△DEF内部的概率为
=(
)2=
;
故答案为:
.
要使该点取自△ABE内部,则所含的基本事件对应的区域为△DEF,
所以所求该点取自△DEF内部的概率就是两部分的面积比,
由已知等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,且
| AD |
| DB |
| 1 |
| 2 |
| BE |
| BD |
| 1 |
| 2 |
∴△ADF,△BED,△CFE都是直角三角形,
∴
| DE |
| BD |
| ||
| 2 |
| DE |
| AB |
| ||
| 3 |
∴该点取自△DEF内部的概率为
| S△DEF |
| S△ABC |
| ||
| 3 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:题考查几何概型的求解,涉及平面图形面积的运算,确定图形的面积是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知二次函数f(x)=ax2+2x+c(x∈R)的值域为[0,+∞),则f(1)的最小值为( )
| A、4 | B、5 | C、6 | D、8 |
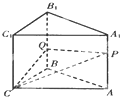 如图,在三棱柱的侧棱A1A和B1B上各有一动点P,Q,且满足A1P=BQ,过P、Q、C三点的截面把棱柱分成两部分,则其上下体积之比为
如图,在三棱柱的侧棱A1A和B1B上各有一动点P,Q,且满足A1P=BQ,过P、Q、C三点的截面把棱柱分成两部分,则其上下体积之比为