题目内容
已知命题p：x1、x2是方程x2-mx-2=0的两个实根，不等式a2-2a≥|x1-x2|对?m∈[0，1]恒成立，若p为真命题，则实数a的取值范围为 ．
考点：命题的真假判断与应用
专题：函数的性质及应用,简易逻辑
分析：利用韦达定理可求得|x1-x2|max=3，从而解关于参数a的不等式即可得出a的取值范围．
解答：
解：∵x1，x2是方程x2-mx-2=0的两个实根，
∴x1+x2=m，x1•x2=-2，
|x1-x2|=
=
，
∴当m∈[0，1]时，|x1-x2|max=3．
由不等式a2-5a-3≥|x1-x2|对任意实数m∈[0，1]恒成立，
可得：a2-2a≥3；
解得：a≥3或a≤-1；
∴命题p为真命题时，实数a的取值范围为（-∞，-1]∪[3，+∞）．
故答案为：（-∞，-1]∪[3，+∞）．
∴x1+x2=m，x1•x2=-2，
|x1-x2|=
| (x1+x2)2-4x1x2 |
| m2+8 |
∴当m∈[0，1]时，|x1-x2|max=3．
由不等式a2-5a-3≥|x1-x2|对任意实数m∈[0，1]恒成立，
可得：a2-2a≥3；
解得：a≥3或a≤-1；
∴命题p为真命题时，实数a的取值范围为（-∞，-1]∪[3，+∞）．
故答案为：（-∞，-1]∪[3，+∞）．
点评：本题考查命题真假性的判断、方程的解的判断、韦达定理及恒成立问题，求得|x1-x2|max=3是关键，也是难点，属于中档题
练习册系列答案
相关题目
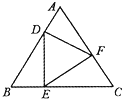如图，等边△DEF的顶点D，E，F分别在等边△ABC的边AB，BC，CA上，且函数f（x）=
的零点个数为（其中a＞0）（ ）
|
| A、0 | B、1 | C、2 | D、3 |