题目内容
在△ABC中,已知a=7,b=5,c=3,则△ABC是 三角形.
考点:余弦定理
专题:解三角形
分析:根据大边对大角判断出角A是最大角,代入余弦定理的推论求出cosA,再求出角A,即可判断出三角形的形状.
解答:
解:在△ABC中知,a=7,b=5,c=3,
则a是最大边,角A是最大角,
由余弦定理的推论得cosA=
=
=-
<0,
则A=120°是钝角,
则△ABC是钝角三角形,
故答案为:钝角.
则a是最大边,角A是最大角,
由余弦定理的推论得cosA=
| b2+c2-a2 |
| 2bc |
| 25+9-49 |
| 2×5×3 |
| 1 |
| 2 |
则A=120°是钝角,
则△ABC是钝角三角形,
故答案为:钝角.
点评:本题主要考查余弦定理的推论的应用,根据三角函数的值求角,属于中档题.

练习册系列答案
相关题目
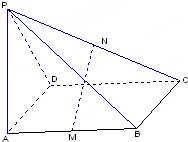 如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点,求证:MN∥平面PAD.
如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点,求证:MN∥平面PAD. 如图,各条棱长均为2的正三棱柱ABC-A1B1C1中,M为A1C1的中点,则三棱锥M-AB1C的体积为
如图,各条棱长均为2的正三棱柱ABC-A1B1C1中,M为A1C1的中点,则三棱锥M-AB1C的体积为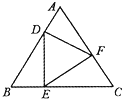 如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,且
如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,且