题目内容
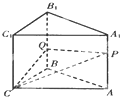 如图,在三棱柱的侧棱A1A和B1B上各有一动点P,Q,且满足A1P=BQ,过P、Q、C三点的截面把棱柱分成两部分,则其上下体积之比为
如图,在三棱柱的侧棱A1A和B1B上各有一动点P,Q,且满足A1P=BQ,过P、Q、C三点的截面把棱柱分成两部分,则其上下体积之比为考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:由已知中A1P=BQ,我们可得四边形PQBA与四边形PQB1A1的面积相等,等于侧面ABPQB1A1的面积的一半,根据等底同高的棱锥体积相等,可将四棱椎C-PQBA的体积转化三棱锥C-ABA1的体积,进而根据同底同高的棱锥体积为棱柱的
,求出四棱椎C-PQBA的体积,进而得到答案.
| 1 |
| 3 |
解答:
 解:设三棱柱ABC-A1B1C1的体积为V,
解:设三棱柱ABC-A1B1C1的体积为V,
∵侧棱AA1和BB1上各有一动点P,Q满足A1P=BQ,
∴四边形PQBA与四边形PQB1A1的面积相等,
故四棱椎C-PQBA的体积等于三棱锥C-ABA1的体积等于
V,
则几何体CPQ-C1B1A1的体积等于
V,
故过P、Q、C三点的截面把棱柱分成两部分,则其体积比为2:1,
故答案为:2:1
 解:设三棱柱ABC-A1B1C1的体积为V,
解:设三棱柱ABC-A1B1C1的体积为V,∵侧棱AA1和BB1上各有一动点P,Q满足A1P=BQ,
∴四边形PQBA与四边形PQB1A1的面积相等,
故四棱椎C-PQBA的体积等于三棱锥C-ABA1的体积等于
| 1 |
| 3 |
则几何体CPQ-C1B1A1的体积等于
| 2 |
| 3 |
故过P、Q、C三点的截面把棱柱分成两部分,则其体积比为2:1,
故答案为:2:1
点评:本题考查的知识点是棱柱的体积,棱锥的体积,其中根据四边形PQBA与四边形PQB1A1的面积相等,等于侧面ABPQB1A1的面积的一半,将四棱椎C-PQBA的体积转化三棱锥C-ABA1的体积,进而根据同底同高的棱锥体积为棱柱的
,求出上下两部分的体积,是解答本题的关键.
| 1 |
| 3 |

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
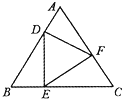 如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,且
如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,且