题目内容
已知二次函数f(x)=ax2+2x+c(x∈R)的值域为[0,+∞),则f(1)的最小值为( )
| A、4 | B、5 | C、6 | D、8 |
考点:二次函数的性质
专题:函数的性质及应用
分析:由题意可知,二次函数f(x)的图象恒在x轴或x轴上方,即a>0,△=0,推出ac的范围,进而利用均值不等式求出a+c的最小值,从而求出f(1)的最小值.
解答:
解:∵二次函数f(x)=ax2+2x+c(x∈R)的值域为[0,+∞),
∴a>0,△=4-4ac=0,
∴a>0,c>0,ac=1,
∴a+c≥2
=2,
当且仅当a=c=1时取等号.
而f(1)=a+c+2≥4
故选:A.
∴a>0,△=4-4ac=0,
∴a>0,c>0,ac=1,
∴a+c≥2
| ac |
当且仅当a=c=1时取等号.
而f(1)=a+c+2≥4
故选:A.
点评:利用基本不等式求函数最值是高考考查的重点内容,对不符合基本不等式形式的应首先变形,然后必须满足三个条件:一正、二定、三相等.同时注意数形结合思想的运用.

练习册系列答案
相关题目
已知a=21.2,b=(
)-0.2,则a,b的大小关系为( )
| 1 |
| 2 |
| A、b<a | B、a<b |
| C、a=b | D、以上都不对 |
下列函数中,在区间(-∞,0]上是增函数的是( )
| A、y=x2-4x+8 | ||||
B、y=log
| ||||
C、y=-
| ||||
D、y=
|
集合M={(x,y)|x∈R,y>0},N={(x,y)|x∈R,y=|x|},则下列关系正确的是( )
| A、M?N | B、N?M |
| C、M=N | D、M与N之间无包含关系 |
函数f(x)=
的零点个数为(其中a>0)( )
|
| A、0 | B、1 | C、2 | D、3 |
若函数f(x)=2x+2-x与g(x)=2x-2-x的定义域均为R,则( )
| A、f(x)与g(x)均为偶函数 |
| B、f(x)为奇函数,g(x)为偶函数 |
| C、f(x)为偶函数,g(x)为奇函数 |
| D、f(x)与g(x)均为奇函数 |
下列函数中,在区间(0,+∞)上为减函数的是( )
A、y=-
| ||
| B、y=ln(x+2) | ||
| C、y=2x | ||
D、y=-
|
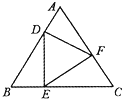 如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,且
如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,且