题目内容
在△ABC中,BC=2,B=
,若△ABC的面积为
,则tanC为 .
| π |
| 3 |
| ||
| 2 |
考点:余弦定理,正弦定理
专题:解三角形
分析:由三角形的面积和条件求出AB的长,再由余弦定理求出AC的长,再由BC2=AB2+AC2判断出△ABC为直角三角形,再求出tanC.
解答:
解:由S△ABC=
BC•BAsinB=
得,BA=1,
由余弦定理得,AC2=AB2+BC2-2AB•BCcosB,
=1+4-4×
=3,得AC=
,
即BC2=AB2+AC2,
∴△ABC为直角三角形,其中A为直角,
则tanC=
=
,
故答案为:
.
| 1 |
| 2 |
| ||
| 2 |
由余弦定理得,AC2=AB2+BC2-2AB•BCcosB,
=1+4-4×
| 1 |
| 2 |
| 3 |
即BC2=AB2+AC2,
∴△ABC为直角三角形,其中A为直角,
则tanC=
| AB |
| AC |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查余弦定理,勾股定理、正切函数,以及三角形的面积公式,熟练掌握公式是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知a=21.2,b=(
)-0.2,则a,b的大小关系为( )
| 1 |
| 2 |
| A、b<a | B、a<b |
| C、a=b | D、以上都不对 |
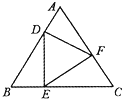 如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,且
如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,且