题目内容
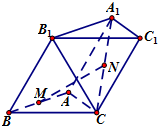 如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.
如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.(Ⅰ)若M、N分别为AB、A1C的中点,求证:MN∥平面BCC1B1;
(Ⅱ)若三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成的角为
60°.问在线段CC1上是否存在一点P,使得平面ABP与底面ABC的所成角为
60°,若存在,求BP的长度,若不存在,说明理由.
考点:用空间向量求平面间的夹角,直线与平面平行的判定,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(Ⅰ)连接AC1,利用三角形的中位线证明:MN∥BC1,然后利用直线与平面平行的判定定理证明即可.
(Ⅱ)过B1作BC的垂线,垂足为O,证明B1O⊥平面ABC,BC⊥AO,以O为原点,BC所在直线为X轴,OA为y轴建立空间直角坐标系,求出平面ABC1的法向量,平面ABC的法向量,利用向量的数量积求解二面角是余弦函数值,从而说明P不存在.
(Ⅱ)过B1作BC的垂线,垂足为O,证明B1O⊥平面ABC,BC⊥AO,以O为原点,BC所在直线为X轴,OA为y轴建立空间直角坐标系,求出平面ABC1的法向量,平面ABC的法向量,利用向量的数量积求解二面角是余弦函数值,从而说明P不存在.
解答:
 解:(I)连接AC1,BC1,∵M、N分别为AB、A1C的中点,
解:(I)连接AC1,BC1,∵M、N分别为AB、A1C的中点,
∴MN
BC1,MN?平面BCC1B1;BC1?平面BCC1B1;
∴MN∥平面BCC1B1;
(II)过B1作BC的垂线,垂足为O,∵侧面BCC1B1⊥底面ABC
所以B1O⊥平面ABC,-----------------------(6分)
所以∠B1BC就是侧棱BB1与底面ABC所成的角,即∠B1BC=60°--(7分)
又AB=AC,所以BC⊥AO,
如图,以O为原点,BC所在直线为X轴,OA为y轴建立空间直角坐标系
则B(-1,0,0),C(1,0,0),A(0,
,0),B1(0,0,
),
∵
=
∴C1(2,0,
),----(8分)
=(1,
,0),
=(3,0,
),
设平面ABC1的法向量为
=(x,y,z)
则
⇒
,
令x=
,则y=-1,x=-3,所以
=(
,-1,-3)---(10分)
又平面ABC的法向量为
=(0,0,1),设平面使得平面ABC1与底面ABC的所成角为α
所以cosα=|cos<
,
>|=
>cos60°=
,
又y=cosx在[0,
]上单调递减,
所以在CC1上不存在点P,使得平面ABP与底面ABC的所成角为60°-------(12分)
 解:(I)连接AC1,BC1,∵M、N分别为AB、A1C的中点,
解:(I)连接AC1,BC1,∵M、N分别为AB、A1C的中点,∴MN
| ∥ |
. |
| 1 |
| 2 |
∴MN∥平面BCC1B1;
(II)过B1作BC的垂线,垂足为O,∵侧面BCC1B1⊥底面ABC
所以B1O⊥平面ABC,-----------------------(6分)
所以∠B1BC就是侧棱BB1与底面ABC所成的角,即∠B1BC=60°--(7分)
又AB=AC,所以BC⊥AO,
如图,以O为原点,BC所在直线为X轴,OA为y轴建立空间直角坐标系
则B(-1,0,0),C(1,0,0),A(0,
| 3 |
| 3 |
∵
| BB1 |
| CC1 |
| 3 |
| BA |
| 3 |
| BC1 |
| 3 |
设平面ABC1的法向量为
| n1 |
则
|
|
令x=
| 3 |
| n1 |
| 3 |
又平面ABC的法向量为
| n2 |
所以cosα=|cos<
| n1 |
| n2 |
| 3 | ||
|
| 1 |
| 2 |
又y=cosx在[0,
| π |
| 2 |
所以在CC1上不存在点P,使得平面ABP与底面ABC的所成角为60°-------(12分)
点评:本题考查直线与平面平行的判定定理的应用,向量法求解二面角的平面角的大小,考查空间想象能力以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
等差数列{an}中a1>0,S5=S8,则当Sn取最大值时n的值是( )
| A、6 | B、7 | C、6或7 | D、不存在 |
要做一个圆锥形的漏斗,其母线长为40cm,要使其体积为最大,则高为( )
A、
| ||||
B、
| ||||
C、10
| ||||
D、
|
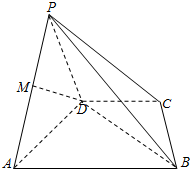 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.