题目内容
两个不同的口袋中,各装有大小、形状完全相同的1个红球、2个黄球.现从每一个口袋中各任取2球,设随机变量ξ为取得红球的个数,则Eξ= .
考点:离散型随机变量的期望与方差
专题:计算题,概率与统计
分析:先确定随机变量ξ的可能取值,然后利用事件的独立性求出ξ在每个可能值下对应的概率,根据随机变量的数学期望的定义求Eξ即可.
解答:
解:由题意ξ的取值为0,1,2. 则P(ξ=0)=
•
=
;P(ξ=1)=2•
•
=
;P(ξ=2)=
•
=
,
所以数学期望:Eξ=0×
+1×
+2×
=
.
故答案为:
.
| ||
|
| ||
|
| 1 |
| 9 |
| ||
|
| ||
|
| 4 |
| 9 |
| ||
|
| ||
|
| 4 |
| 9 |
所以数学期望:Eξ=0×
| 1 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题考查事件的独立性、离散型随机变量的概率分布列与数学期望,比较基础.

练习册系列答案
相关题目
当x>0,y>0,
+
=1时,x+y的最小值为( )
| 1 |
| x |
| 9 |
| y |
| A、10 | B、12 | C、14 | D、16 |
下面是一个2×2列联表,则a-b的值等于( )
| y1 | y2 | 总计 | |
| x1 | c | a | 69 |
| x2 | b | d | f |
| 总计 | e | 65 | 99 |
| A、45 | B、35 | C、34 | D、25 |
设函数f(x)的导函数为f′(x),对任意x∈R,都有xf′(x)>f(x)成立,则( )
| A、3f(2)>2f(3) |
| B、3f(2)=2f(3) |
| C、3f(2)<2f(3) |
| D、3f(2)与2f(3)的大小不确定 |
要做一个圆锥形的漏斗,其母线长为40cm,要使其体积为最大,则高为( )
A、
| ||||
B、
| ||||
C、10
| ||||
D、
|
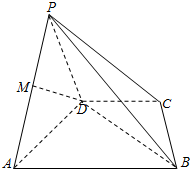 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.