题目内容
在△ABC中,AB=2,∠C=45°,求△ABC的面积的最大值.
考点:余弦定理
专题:解三角形
分析:由余弦定理及基本不等式可得结论,注意验证等号成立的条件.
解答:
解:∵在△ABC中,AB=2,∠C=45°,
由余弦定理及基本不等式得4=a2+b2-2abcos45°≥2ab-
ab
∴ab≤
,∴S=
absinc≤
×
×
=
+1.
当且仅当a=b时取等号,
∴△ABC的面积的最大值为
+1
由余弦定理及基本不等式得4=a2+b2-2abcos45°≥2ab-
| 2 |
∴ab≤
| 4 | ||
2-
|
| 1 |
| 2 |
| 1 |
| 2 |
| 4 | ||
2-
|
| ||
| 2 |
| 2 |
当且仅当a=b时取等号,
∴△ABC的面积的最大值为
| 2 |
点评:本题考查余弦定理,涉及基本不等式的应用,属中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
下面是一个2×2列联表,则a-b的值等于( )
| y1 | y2 | 总计 | |
| x1 | c | a | 69 |
| x2 | b | d | f |
| 总计 | e | 65 | 99 |
| A、45 | B、35 | C、34 | D、25 |
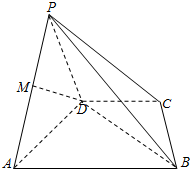 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.