题目内容
设l、m是两条不同的直线,α、β是两个不同的平面,则下列论述正确的是( )
| A、若l∥α,m∥α,则l∥m |
| B、若l∥α,l∥β,则α∥β |
| C、若l∥m,l⊥α,则m⊥α |
| D、若l∥α,α⊥β,则l⊥β |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系进行判断.
解答:
解:由l、m是两条不同的直线,α、β是两个不同的平面,知:
若l∥α,m∥α,则l与m相交、平行或异面,故A错误;
若l∥α,l∥β,则α与β平行或相交,故B错误;
若l∥m,l⊥α,则由直线与平面垂直的判定定理知m⊥α,故C正确;
若l∥α,α⊥β,则l相交β、平行或l?β,故D错误.
故选:C.
若l∥α,m∥α,则l与m相交、平行或异面,故A错误;
若l∥α,l∥β,则α与β平行或相交,故B错误;
若l∥m,l⊥α,则由直线与平面垂直的判定定理知m⊥α,故C正确;
若l∥α,α⊥β,则l相交β、平行或l?β,故D错误.
故选:C.
点评:本题考查命题的真假判断,是基础题,解题时要认真审题,注意空间能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )
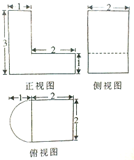

A、4+
| ||
B、4+
| ||
C、4+
| ||
| D、4+π |
a,b∈R,下列不等式中一定成立的是( )
| A、若a>b,则a2>b2 | ||||
B、若a>b,则
| ||||
| C、若|a|>b,则a2>b2 | ||||
| D、若a>|b|,则a2>b2 |
sin(-
)的值为( )
| 25π |
| 6 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
设随机变量X~B(2,P),随机变量Y~B(3,P),若P(X≥1)=
,则P(Y≥1)等于( )
| 5 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|

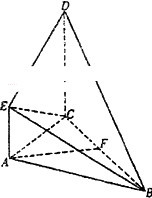 如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.
如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.