题目内容
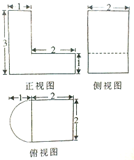
某几何体的三视图如图所示，则该几何体的体积为（ ）
A、4+
| ||
B、4+
| ||
C、4+
| ||
| D、4+π |
考点：组合几何体的面积、体积问题,由三视图求面积、体积
专题：空间位置关系与距离
分析：几何体是一个简单组合体，左侧是一个半圆柱，底面的半径是1，高为：3，右侧是一个正四棱柱，四棱柱的底面是一个正方形，边长是2，四棱柱的高是1，根据体积公式得到结果．
解答：
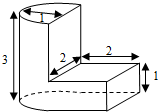解：由三视图知，几何体是一个简单组合体，左侧是一个半圆柱，底面的半径是1，高为：3，
右侧是一个正四棱柱，四棱柱的底面是一个正方形，边长是2，四棱柱的高是1，
∴组合体的体积是：
π×12×3+2×2×1=4+
，
故选：B．
解：由三视图知，几何体是一个简单组合体，左侧是一个半圆柱，底面的半径是1，高为：3，右侧是一个正四棱柱，四棱柱的底面是一个正方形，边长是2，四棱柱的高是1，
∴组合体的体积是：
| 1 |
| 2 |
| 3π |
| 2 |
故选：B．
点评：本题考查由三视图求几何体的体积，考查由三视图还原直观图，本题是一个基础题，题目的运算量比较小，若出现是一个送分题目．
练习册系列答案
相关题目
条件甲：“a＞0且b＞0”，条件乙：“方程
-
=1表示双曲线”，那么甲是乙的（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
对任意实数a，b定义运算“?”：a?b=
，设f（x）=（x2-1）?（4+x），若函数y=f（x）+k的图象与x轴恰有三个不同交点，则k的取值范围是（ ）
|
| A、（-2，1） |
| B、[0，1] |
| C、[-2，0） |
| D、[-2，1） |
设集合A={x|y=lgx}，B={x|x≤1}，则A∩B=（ ）
| A、（0，+∞） |
| B、[1，+∞） |
| C、（0，1] |
| D、（-∞，1] |
已知a是1、2的等差中项，b是-1、-16的等比中项，则ab=（ ）
| A、6 | B、-6 | C、±6 | D、±12 |
已知集合A={x|
≥1}，B={x|y=
}，则A∪B=（ ）
| 1 |
| x+1 |
| x2-1 |
| A、（-∞，1] |
| B、（-1，0）∪[1，+∞） |
| C、（-∞，0）∪[1，+∞） |
| D、（-∞，0]∪[1，+∞） |
设l、m是两条不同的直线，α、β是两个不同的平面，则下列论述正确的是（ ）
| A、若l∥α，m∥α，则l∥m |
| B、若l∥α，l∥β，则α∥β |
| C、若l∥m，l⊥α，则m⊥α |
| D、若l∥α，α⊥β，则l⊥β |