题目内容
已知在△ABC中,AB=AC,∠CAB=
,M为△ABC的外心,且
=λ
+μ
,则λ+2μ= .
| π |
| 6 |
| CM |
| CA |
| CB |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
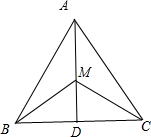
分析:连接AM,BM,延长AM交BC于D,所以根据已知条件即知D为BC边的中点,并且AD⊥BC,∠BMC=
,所以△MBC是等边三角形,设外接圆半径为r,在
=λ
+μ
两边同乘以
,根据数量积的计算公式并结合图形可得到
r2=
r2+μr2,所以到这即求出了λ+2μ=1.
| π |
| 3 |
| CM |
| CA |
| CB |
| CB |
| 1 |
| 2 |
| λ |
| 2 |
解答:
解:如图,连接AM,BM,延长AM交BC于D,由已知条件知D为BC中点,且AD⊥BC;
 ∵∠CAB=
∵∠CAB=
,∴∠BMC=
,又MB=MC;
∴△MBC为等边三角形,设外接圆半径为r,则|BC|=r;
∴
•
=λ
•
+μ
2;
∴
r2=
r2+μr2;
∴λ+2μ=1.
故答案为:1.
 ∵∠CAB=
∵∠CAB=| π |
| 6 |
| π |
| 3 |
∴△MBC为等边三角形,设外接圆半径为r,则|BC|=r;
∴
| CM |
| CB |
| CA |
| CB |
| CB |
∴
| 1 |
| 2 |
| λ |
| 2 |
∴λ+2μ=1.
故答案为:1.
点评:考查三角形外接圆的概念,以及圆心角和圆周角的关系,以及数量积的计算公式:
•
=|
||
|cos<
,
>.
| a |
| b |
| a |
| b |
| a |
| b |

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
若对任意的实数x,不等式|x+1|-|x-2|>a恒成立,则实数a的取值范围为( )
| A、(-∞,3) |
| B、(-∞,3] |
| C、(-∞,-3) |
| D、(-∞,-3] |
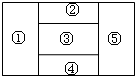 如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着方法共有( )种.
如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着方法共有( )种.| A、36 | B、24 | C、72 | D、48 |
若x3=a0+a1(x-2)+a2(x-2)2+a3(x-2)3,则a2的值为( )
| A、12 | B、9 | C、6 | D、3 |
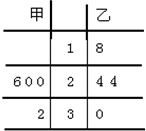 甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如图所示:
甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如图所示: