题目内容
定义在R上的函数f(x)满足f(x+6)=f(x).当-3≤x<-1时,f(x)=-(x+2)2,当-1≤x<3时,f(x)=x.则f(1)+f(2)+…+f(2014)=( )
| A、335 | B、336 |
| C、337 | D、2014 |
考点:抽象函数及其应用,函数的值
专题:函数的性质及应用
分析:运用函数的周期性得f(x+6)=f(x),求出f(1),f(2),f(3),f(4),f(5),f(6)的值,再求和,最后运用周期性求解f(1)+f(2)+…+f(2013)+f(2014)=335+f(1)+f(2)+f(3)+f(4)可得答案.
解答:
解:∵函数f(x)的定义域为R,若函数f(x)的周期6,
∴f(x+6)=f(x),
∵-3≤x<-1时,f(x)=-(x+2)2,当-1≤x<3时,f(x)=x,
∴f(1)=1,f(2)=2,f(3)=f(6-3)=f(-3)=-(-3+2)2=-1,
f(4)=f(6-2)=f(-2)=-(-2+2)2=0,
f(5)=f(6-1)=f(-1)=-(-1+2)2=-1,
f(6)=f(0)=0,
f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=1
∴f(1)+f(2)+…+f(2013)+f(2014)=335+f(1)+f(2)+f(3)+f(4)=337
故选:C.
∴f(x+6)=f(x),
∵-3≤x<-1时,f(x)=-(x+2)2,当-1≤x<3时,f(x)=x,
∴f(1)=1,f(2)=2,f(3)=f(6-3)=f(-3)=-(-3+2)2=-1,
f(4)=f(6-2)=f(-2)=-(-2+2)2=0,
f(5)=f(6-1)=f(-1)=-(-1+2)2=-1,
f(6)=f(0)=0,
f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=1
∴f(1)+f(2)+…+f(2013)+f(2014)=335+f(1)+f(2)+f(3)+f(4)=337
故选:C.
点评:本题考查了函数的性质,抽象函数的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
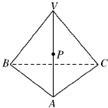 一正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,若木块的棱长为a,则截面面积为( )
一正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,若木块的棱长为a,则截面面积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
若对任意的实数x,不等式|x+1|-|x-2|>a恒成立,则实数a的取值范围为( )
| A、(-∞,3) |
| B、(-∞,3] |
| C、(-∞,-3) |
| D、(-∞,-3] |
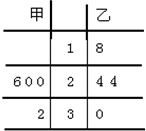 甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如图所示:
甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如图所示: 如图,已知?ABCD中,E是AB的中点,F是BE的中点,DF,CE相较于点O,已知
如图,已知?ABCD中,E是AB的中点,F是BE的中点,DF,CE相较于点O,已知