题目内容
设点A是抛物线y2=4x上一点,点B(1.0),点M是线段AB的中点,若|AB|=3,则M 到直线x=-1的距离为( )
| A、5 | ||
B、
| ||
| C、2 | ||
D、
|
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,点B(1.0)是焦点,直线x=-1是准线.利用抛物线的定义,可得A到准线的距离为3,利用梯形中位线的性质,可得M到直线x=-1的距离.
解答:
解:由题意,点B(1.0)是焦点,直线x=-1是准线.
利用抛物线的定义,可得A到准线的距离为3,
∵点M是线段AB的中点,
∴M到直线x=-1的距离为
=
.
故选:D.
利用抛物线的定义,可得A到准线的距离为3,
∵点M是线段AB的中点,
∴M到直线x=-1的距离为
| 2+3 |
| 2 |
| 5 |
| 2 |
故选:D.
点评:本题考查M到直线x=-1的距离,考查抛物线的定义,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
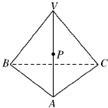 一正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,若木块的棱长为a,则截面面积为( )
一正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,若木块的棱长为a,则截面面积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
若x3=a0+a1(x-2)+a2(x-2)2+a3(x-2)3,则a2的值为( )
| A、12 | B、9 | C、6 | D、3 |
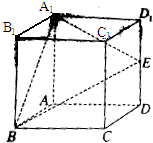 如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正弦值构成的集合是 ( )
如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正弦值构成的集合是 ( )| A、{2} | ||||||||
B、
| ||||||||
C、{t|
| ||||||||
D、{t|
|
若向量
与
不共线,
•
≠0,且
=
-
,则向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| c |
| a |
(
| ||||||
|
| a |
| c |
A、
| ||
B、
| ||
C、
| ||
| D、0 |
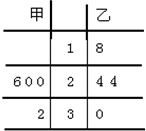 甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如图所示:
甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如图所示: 如图,已知?ABCD中,E是AB的中点,F是BE的中点,DF,CE相较于点O,已知
如图,已知?ABCD中,E是AB的中点,F是BE的中点,DF,CE相较于点O,已知