题目内容
某厂去年年底的产值为a,今年前两个月产值总体下降了36%,要想后两个月产值恢复到原来水平,则这两个月月平均增长( )
| A、18% | B、25% |
| C、28% | D、以上都不对 |
考点:根式与分数指数幂的互化及其化简运算
专题:函数的性质及应用
分析:若月初产值基数为a,月平均增长率为P,则经过n月的月产值为a(1+p)n,进而得到答案.
解答:
解:∵某厂去年年底的产值为a,今年前两个月产值总体下降了36%,
故月初产值基数为a(1-36%)=0.64a,
若要想后两个月产值恢复到原来水平,
不妨设月平均增长率为P,
则0.64a(1+p)2=a,
即(1+p)2=
,
解得P=25%,
故选:B
故月初产值基数为a(1-36%)=0.64a,
若要想后两个月产值恢复到原来水平,
不妨设月平均增长率为P,
则0.64a(1+p)2=a,
即(1+p)2=
| 100 |
| 64 |
解得P=25%,
故选:B
点评:增长率问题属于指数函数模型,公式类似于等比数列的通项公式,有一种误区是将它看成等差数列模型,要谨防出现第n个月的产值an=a(1+np)这样的错误.

练习册系列答案
相关题目
已知数列{an}的通项公式an=logn+1(n+2)(n∈N+),记Jn=a1•a2•a3•…•an为数列{an}的前n项积.定义能使Jn为整数的正整数n为劣数,则在区间(1,2014)内所有的劣数和为( )
| A、2026 | B、2046 |
| C、1024 | D、1022 |
已知|
|=6,|
|=4,则|
|的取值范围为( )
| AB |
| AC |
| BC |
| A、(2,8) |
| B、[2,8] |
| C、(2,10) |
| D、[2,10] |
已知圆C:x2+y2-4x=0,l过点P(1,1)的直线,则( )
| A、l与C相交 |
| B、l与C相切 |
| C、l与C相离 |
| D、以上三个选项均有可能 |
如图,AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,则
=( )
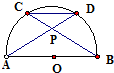
| CD |
| AB |

| A、sinα | ||
| B、cosα | ||
| C、tanα | ||
D、
|
已知sinα-cosα=-
,则tanα=( )
| 2 |
| A、-1 | ||||
| B、1 | ||||
C、-
| ||||
D、
|
在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )
| A、120° | B、100° |
| C、80° | D、60° |
已知n为正偶数,用数学归纳法证明时,若已假设n=k(k≥2,且k为偶数)时等式成立,则还需利用归纳假设再证( )
| A、n=k+1时等式成立 |
| B、n=k+2时等式成立 |
| C、n=2k+2时等式成立 |
| D、n=2(k+2)时等式成立 |