题目内容
在⊙O的内接四边形ABCD中，∠BOD=120°，那么∠BCD是（ ）
| A、120° | B、100° |
| C、80° | D、60° |
考点：圆內接多边形的性质与判定
专题：立体几何
分析：画出图形，根据图形，结合圆内接四边形的知识，进行解答，即可得出正确的答案．
解答：
解：画出图形，如图所示，
∵⊙O的内接四边形ABCD中，∠BOD=120°，
∴∠A=
∠BOD=60°，
∴∠BCD=180°-∠A=120°．
故选：A．
∵⊙O的内接四边形ABCD中，∠BOD=120°，
∴∠A=
| 1 |
| 2 |
∴∠BCD=180°-∠A=120°．
故选：A．
点评：本题考查了圆内接四边形的知识以及应用问题，解题时应画出图形，结合图形解答问题，是基础题．
练习册系列答案
相关题目
已知f（x）=2x3-6x2+a（a是常数）在[-2，2]上有最大值11，那么在[-2，2]上f（x）的最小值是（ ）
| A、-5 | B、-11 |
| C、-29 | D、-37 |
曲线y=
在点（3，2）处的切线与直线ax-y+1=0垂直，则a的值为（ ）
| x+1 |
| x-1 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
某厂去年年底的产值为a，今年前两个月产值总体下降了36%，要想后两个月产值恢复到原来水平，则这两个月月平均增长（ ）
| A、18% | B、25% |
| C、28% | D、以上都不对 |
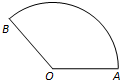如图，扇形OAB中，OA=OB=1， |
| AB |
|
| AB |
A、1-
| ||
B、2-
| ||
C、1-
| ||
D、
|
已知集合A={x|x2+2x-3≤0}，B={x|x2≤4}，则A∩B=（ ）
| A、{x|-2≤x≤1} |
| B、{x|0≤x≤1} |
| C、{x|-3≤x≤2} |
| D、{x|1≤x≤2} |
已知集合A={x|x2-11x+10≤0}，B={y|y=lgx，x∈A}，则A∪B=（ ）
| A、[0，1] |
| B、[1，10] |
| C、{1} |
| D、[0，10] |
在数列{an}中，a1=1，an+1=
（n∈N*），猜想这个数列的通项公式为（ ）
| 2an |
| 2+an |
| A、an=n | ||
B、an=
| ||
C、an=
| ||
D、an=
|