题目内容
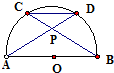
如图,AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,则
=( )
| CD |
| AB |

| A、sinα | ||
| B、cosα | ||
| C、tanα | ||
D、
|
考点:与圆有关的比例线段
专题:直线与圆,立体几何
分析:连结BD,由已知条件推导出△CPD∽△APB,△ADP是直角三角形,PB是斜边,由此能求出
=cosa.
| CD |
| AB |
解答:
解:连结BD,
∵∠CDA和∠CBA对应同一段圆弧AC,
∴∠CDA=∠CBA,
同理∠DCB=∠DAB,
又∠APB和∠CPD是对等角,∴∠APB=∠CPD,
∴△CPD∽△APB,∴
=
,
∵∠ADB对应的弦AB是半圆O的直径,
∴∠ADB是直角,
∴△ADP是直角三角形,PB是斜边,
∴
=cosα,∴
=cosa.
故选:B.
∵∠CDA和∠CBA对应同一段圆弧AC,
∴∠CDA=∠CBA,

同理∠DCB=∠DAB,
又∠APB和∠CPD是对等角,∴∠APB=∠CPD,
∴△CPD∽△APB,∴
| CD |
| AB |
| PD |
| PB |
∵∠ADB对应的弦AB是半圆O的直径,
∴∠ADB是直角,
∴△ADP是直角三角形,PB是斜边,
∴
| PD |
| PB |
| CD |
| AB |
故选:B.
点评:本题考查两条线段的比值的求法,是中档题,解题时要认真审题,注意相似三角形的性质的灵活运用.

练习册系列答案
相关题目
双曲线
-y2=1的焦距为( )
| x2 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
曲线y=
在点(3,2)处的切线与直线ax-y+1=0垂直,则a的值为( )
| x+1 |
| x-1 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
已知lg(x+y)+lg(2x+3y)-lg3=lg4+lgx+lgy,则
的值( )
| x |
| y |
| A、3 | ||
B、3或
| ||
C、
| ||
| D、3或0 |
某厂去年年底的产值为a,今年前两个月产值总体下降了36%,要想后两个月产值恢复到原来水平,则这两个月月平均增长( )
| A、18% | B、25% |
| C、28% | D、以上都不对 |
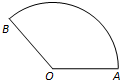 如图,扇形OAB中,OA=OB=1,
如图,扇形OAB中,OA=OB=1, |
| AB |
 |
| AB |
A、1-
| ||
B、2-
| ||
C、1-
| ||
D、
|
已知集合A={x|x2-11x+10≤0},B={y|y=lgx,x∈A},则A∪B=( )
| A、[0,1] |
| B、[1,10] |
| C、{1} |
| D、[0,10] |
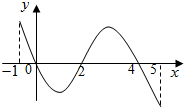 已知函数f(x)的定义域为[-1,5],部分对应值如下表:
已知函数f(x)的定义域为[-1,5],部分对应值如下表: