题目内容
 某种产品特约经销商根据以往当地的需求情况,得出如图该种产品日需求量的频率分布直方图.
某种产品特约经销商根据以往当地的需求情况,得出如图该种产品日需求量的频率分布直方图.(Ⅰ)求图中a的值,并估计日需求量的众数;
(Ⅱ)某日,经销商购进130件该种产品,根据近期市场行情,当天每售出1件能获利30元,未售出的部分,每件亏损20元.设当天的需求量为x件(100≤x≤150),纯利润为S元.
(ⅰ)将S表示为x的函数;
(ⅱ)根据直方图估计当天纯利润S不少于3400元的概率.
考点:古典概型及其概率计算公式,函数解析式的求解及常用方法,频率分布直方图
专题:计算题,概率与统计
分析:(I)根据所有小矩形的面积之和为1,求得第四组的频率,再根据小矩形的高=
求a的值;
(II)利用分段函数写出S关于x的函数;根据S≥3400得x的范围,利用频率分布直方图求数据在范围内的频率及可得概率.
| 频率 |
| 组距 |
(II)利用分段函数写出S关于x的函数;根据S≥3400得x的范围,利用频率分布直方图求数据在范围内的频率及可得概率.
解答:
解:(Ⅰ)由直方图可知:(0.013+0.015+0.017+a+0.030)×10=1,∴a=0.025,
∵
=125,
∴估计日需求量的众数为125件;
(Ⅱ)(ⅰ)当100≤x<130时,S=30x-20(130-x)=50x-2600,
当130≤x≤150时,S=30×130=3900,
∴S=
;
(ⅱ)若S≥3400由50x-2600≥3400得x≥120,
∵100≤x≤150,
∴120≤x≤150,
∴由直方图可知当120≤x≤150时的频率是(0.030+0.025+0.015)×10=0.7,
∴可估计当天纯利润S不少于3400元的概率是0.7.
∵
| 120+130 |
| 2 |
∴估计日需求量的众数为125件;
(Ⅱ)(ⅰ)当100≤x<130时,S=30x-20(130-x)=50x-2600,
当130≤x≤150时,S=30×130=3900,
∴S=
|
(ⅱ)若S≥3400由50x-2600≥3400得x≥120,
∵100≤x≤150,
∴120≤x≤150,
∴由直方图可知当120≤x≤150时的频率是(0.030+0.025+0.015)×10=0.7,
∴可估计当天纯利润S不少于3400元的概率是0.7.
点评:本题考查了由频率分布直方图求频率与众数,考查了分段函数的值域与定义域,在频率分布直方图中小矩形的高=
,所有小矩形的面积之和为1.
| 频率 |
| 组距 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
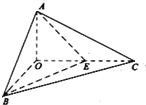 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.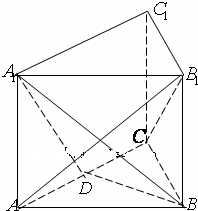 如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱垂直于底面,侧棱长为
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱垂直于底面,侧棱长为