题目内容
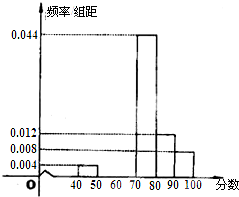 南昌二中某学生社团为了选拔若干名社团义务宣传员,从300名志愿者中随机抽取了50名进行有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列,如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.
南昌二中某学生社团为了选拔若干名社团义务宣传员,从300名志愿者中随机抽取了50名进行有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列,如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.(1)求第二组、第三组的频率并补充完整频率分布直方图;
(2)由所抽取志愿者的成绩分布,估计该社团的300名志愿者中有多少人可以入选为义务宣传员?
考点:频率分布直方图
专题:计算题,概率与统计
分析:(1)由频率分布直方图可得二、三组的频率,再根据频数=频率×样本容量得二、三两组的人数和,利用前三组人数成等差数列可得二、三组的频率及对应小矩形的高;
(2)利用对应小矩形的面积和求成绩不低于66分的频率,根据总体人数求可以入选为义务宣传员的人数.
(2)利用对应小矩形的面积和求成绩不低于66分的频率,根据总体人数求可以入选为义务宣传员的人数.
解答:
解:(1)二、三两组的人数和为50-(0.004+0.044+0.012+0.008)×10×50=16,
设公差为d,第一组人数为0.004×10×50=2人,则2+d+2+2d=16,解得d=4,
∴第二组的频率是
=0.12,对应小矩形的高为0.012;
第三组的频率是
=0.20,对应小矩形的高为0.020,补全频率分布直方图如图:
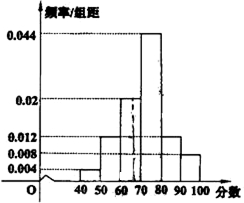
(2)成绩不低于6(6分)的频率为(0.008+0.012+0.044+
×0.020)×10=0.72,
∴估计可成为义务宣传员的人数为0.72×300=216人.
设公差为d,第一组人数为0.004×10×50=2人,则2+d+2+2d=16,解得d=4,
∴第二组的频率是
| 6 |
| 50 |
第三组的频率是
| 10 |
| 50 |

(2)成绩不低于6(6分)的频率为(0.008+0.012+0.044+
| 4 |
| 10 |
∴估计可成为义务宣传员的人数为0.72×300=216人.
点评:本题考查了频率分布直方图的相关知识,在频率分布直方图中频率=小矩形的面积=小矩形的高×组距=
,所有小矩形的面积之和为1.
| 频数 |
| 样本容量 |

练习册系列答案
相关题目
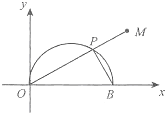 在直角坐标xoy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,如图,曲线C与x轴交于O,B两点,P是曲线C在x轴上方图象上任意一点,连结OP并延长至M,使PM=PB,当P变化时,求动点M的轨迹的长度.
在直角坐标xoy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,如图,曲线C与x轴交于O,B两点,P是曲线C在x轴上方图象上任意一点,连结OP并延长至M,使PM=PB,当P变化时,求动点M的轨迹的长度. 如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,
如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,
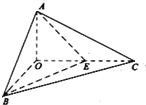 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.