题目内容
已知函数f(x)=e2x2-1,若f[cos(
+θ)]=1,则θ的值为 .
| π |
| 2 |
考点:函数的值
专题:函数的性质及应用
分析:根据条件结合指数方程的求解,即可得到结论.
解答:
解:由f[cos(
+θ)]=1得f(-sinθ)=1,
即e2sin2θ-1=1,
则2sin2θ-1=0,
即sin2θ=
,则sinθ=±
,
解得θ=
+
,k∈Z,
故答案为:θ=
+
,k∈Z
| π |
| 2 |
即e2sin2θ-1=1,
则2sin2θ-1=0,
即sin2θ=
| 1 |
| 2 |
| ||
| 2 |
解得θ=
| kπ |
| 2 |
| π |
| 4 |
故答案为:θ=
| kπ |
| 2 |
| π |
| 4 |
点评:本题主要考查函数值的计算,根据指数方程和三角函数的性质是解决本题的关键.

练习册系列答案
相关题目
命题P:?x∈R,ax2+ax+1≥0为真命题,则实数a的取值范围是( )
| A、(0,4] |
| B、(-∞,4)∪(4,+∞) |
| C、(-∞,0]∪[4,+∞) |
| D、[0,4] |
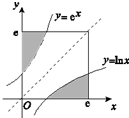 如图,由x=0,x=e,y=0,y=e,y=lnx,y=ex六条曲线共同围成的面积为
如图,由x=0,x=e,y=0,y=e,y=lnx,y=ex六条曲线共同围成的面积为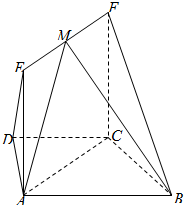 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠CBA=30°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=3.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠CBA=30°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=3.