题目内容
已知f(x)=logax,g(x)=2loga(2x+t-2)(a>0,a≠1,t∈R)
(1)当t=4,x∈[1,2],且F(x)=g(x)-f(x)有最小值2时,求a的值;
(2)当0<a<1,x∈[1,2]时,有f(x)≥g(x)恒成立,求实数t的取值范围;
(3)当0<a<1,存在x∈[1,2],使f(x)≥g(x)成立,求实数t的取值范围.
(1)当t=4,x∈[1,2],且F(x)=g(x)-f(x)有最小值2时,求a的值;
(2)当0<a<1,x∈[1,2]时,有f(x)≥g(x)恒成立,求实数t的取值范围;
(3)当0<a<1,存在x∈[1,2],使f(x)≥g(x)成立,求实数t的取值范围.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)将t=4代入F(x),求出其定义域,先判断其为增函数,根据题意函数F(x)=g(x)-f(x)有最小值2,列出等式,求a的值;
(2)当0<a<1时,若f(x)≥g(x)对x∈[1,2]恒成立,即loga
≥loga(2x+t-2)对x∈[1,2]恒成立,即
≤2x+t-2对x∈[1,2]恒成立,即t≥
-2x+2对x∈[1,2]恒成立,求出当x∈[1,2]时,y=
-2x+2的最大值,可得答案;
(3)当0<a<1时,若存在x∈[1,2],使f(x)≥g(x)成立,即
≤2x+t-2在x∈[1,2]上有解,即t≥
-2x+2在x∈[1,2]上有解,求出当x∈[1,2]时,y=
-2x+2的最小值,可得答案;
(2)当0<a<1时,若f(x)≥g(x)对x∈[1,2]恒成立,即loga
| x |
| x |
| x |
| x |
(3)当0<a<1时,若存在x∈[1,2],使f(x)≥g(x)成立,即
| x |
| x |
| x |
解答:
解:(1)由题意,t=4时,F(x)=g(x)-f(x)=loga
,x∈[1,2],
令h(x)=
=4(x+
+2),
由对勾函数的图象和性质可得:y=x+
在[1,2]上为增函数,
∴x+
∈[2,
],
∴h(x)∈[16,18],
当0<a<1时,F(x)的最小值为:loga18=2,解得a=3
(舍去),
当a>1时,F(x)的最小值为:loga16=2,解得a=4
(2)当0<a<1时,
∵f(x)≥g(x)对x∈[1,2]恒成立,
∴loga
≥loga(2x+t-2)对x∈[1,2]恒成立,
即
≤2x+t-2对x∈[1,2]恒成立,
即t≥
-2x+2对x∈[1,2]恒成立,
当x∈[1,2]时,y=
-2x+2=-2(
-
)2+
,在x=1时取最大值1,
故t≥1;
(3)当0<a<1时,
存在x∈[1,2],使f(x)≥g(x)成立,
即
≤2x+t-2在x∈[1,2]上有解,
即t≥
-2x+2在x∈[1,2]上有解,
当x∈[1,2]时,y=
-2x+2=-2(
-
)2+
在x=2时取最小值
-2,
故t≥
-2;
| (2x+2)2 |
| x |
令h(x)=
| (2x+2)2 |
| x |
| 1 |
| x |
由对勾函数的图象和性质可得:y=x+
| 1 |
| x |
∴x+
| 1 |
| x |
| 5 |
| 2 |
∴h(x)∈[16,18],
当0<a<1时,F(x)的最小值为:loga18=2,解得a=3
| 2 |
当a>1时,F(x)的最小值为:loga16=2,解得a=4
(2)当0<a<1时,
∵f(x)≥g(x)对x∈[1,2]恒成立,
∴loga
| x |
即
| x |
即t≥
| x |
当x∈[1,2]时,y=
| x |
| x |
| 1 |
| 4 |
| 17 |
| 8 |
故t≥1;
(3)当0<a<1时,
存在x∈[1,2],使f(x)≥g(x)成立,
即
| x |
即t≥
| x |
当x∈[1,2]时,y=
| x |
| x |
| 1 |
| 4 |
| 17 |
| 8 |
| 2 |
故t≥
| 2 |
点评:此题主要考查对数函数的性质及其应用,解题的过程中利用到了转化的思想,考查的知识点比较大,是一道难题;

练习册系列答案
相关题目
 过椭圆C:
过椭圆C: 如图,在边长为1的正方形中随机撒1000粒豆子,有230粒落在阴影部分,据此估计阴影部分的面积为
如图,在边长为1的正方形中随机撒1000粒豆子,有230粒落在阴影部分,据此估计阴影部分的面积为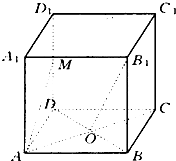 在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,M为D1D的中点.
在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,M为D1D的中点.