题目内容
定义某种运算⊙，S=a⊙b，的运算原理如图所示，则式子6⊙3+2⊙4=（ ）
| A、16 | B、14 | C、10 | D、6 |
考点：程序框图
专题：算法和程序框图
分析：算法的功能是求S=a⊙b=
的值，代入数值计算可得答案．
|
解答：
解：由程序框图知，算法的功能是求S=a⊙b=
的值，
∴6⊙3=6×2=12；
2⊙4=4×1=4．
∴6⊙3+2⊙4=16．
故选：A．
|
∴6⊙3=6×2=12；
2⊙4=4×1=4．
∴6⊙3+2⊙4=16．
故选：A．
点评：本题考查了选择结构的程序框图，根据框图的流程判断算法的功能是关键．
练习册系列答案
相关题目
执行如图所示的程序框图，若输入n的值为5，则输出s的值是（ ）
| A、4 | B、7 | C、11 | D、16 |
“m=3”是“直线（m-1）x+2my+1=0与直线（m+3）x-（m-1）y+3=0相互垂直”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
数列1
，3
，5
，7
，…的一个通项公式为an=（ ）
| 1 |
| 3 |
| 2 |
| 5 |
| 3 |
| 7 |
| 4 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
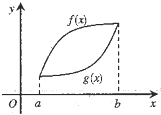已知函数f（x）和g（x）在区间[a，b]上的图象如图所示，那么下列说法正确的是（ ）| A、f（x）在a到b之间的平均变化率大于g（x）在a到b之间的平均变化率 |
| B、f（x）在a到b之间的平均变化率小于g（x）在a到b之间的平均变化率 |
| C、对于任意x0∈（a，b），函数f（x）在x=x0处的瞬时变化率总大于函数g（x）在x=x0处的瞬时变化率 |
| D、存在x0∈（a，b），使得函数f（x）在x=x0处的瞬时变化率小于函数g（x）在x=x0处的瞬时变化率 |
若函数f（x）=asinωx-cosωx的相邻两个零点的距离为π，且它的一条对称轴为x=
π，则f（-
）等于（ ）
| 2 |
| 3 |
| π |
| 3 |
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
设z=1-i（i是虚数单位），则
=（ ）
| 1 |
| z |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|