题目内容
若△ABC的三个顶点是A（-5，0），B（3，-3），C（0，2），则△ABC的面积为（ ）
A、
| ||
| B、31 | ||
| C、23 | ||
| D、46 |
考点：正弦定理,直线的一般式方程,点到直线的距离公式
专题：直线与圆
分析：利用两点间的距离公式求得AC的长度，然后根据A，C的坐标求得直线AC的方程，进而利用点到直线的求得B到直线AC的距离，即三角形的高，最后利用面积公式求得答案．
解答：
解：|AC|=
=
设AC所在直线方程为y=kx+b，把点A，C的坐标代入可求得
，求得b=2，k=
，
∴直线AC的方程为y=
x+2，即2x-5y+10=0，
∴点B到直线AC的距离为
=
∴S△ABC=
×
×
=
．
故选：A．
| 52+22 |
| 29 |
设AC所在直线方程为y=kx+b，把点A，C的坐标代入可求得
|
| 2 |
| 5 |
∴直线AC的方程为y=
| 2 |
| 5 |
∴点B到直线AC的距离为
| |3×2+3×5+10| | ||
|
| 31 | ||
|
∴S△ABC=
| 1 |
| 2 |
| 29 |
| 31 | ||
|
| 31 |
| 2 |
故选：A．
点评：本题主要考查了直线的一般方程，点到直线的距离，点到点的距离等知识，注意利用数形结合的思想．
练习册系列答案
相关题目
如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A′DE（A′∉平面ABC）是△ADE绕DE旋转过程中的一个图形，有下列命题：①平面A′FG⊥平面ABC；
②BC∥平面A′DE；
③三棱锥A′-DEF的体积最大值为
| 1 |
| 64 |
④动点A′在平面ABC上的射影在线段AF上；
⑤二面角A′-DE-F大小的范围是[0，
| π |
| 2 |
其中正确的命题是（ ）
| A、①③④ | B、①②③④ |
| C、①②③⑤ | D、①②③④⑤ |
“m=3”是“直线（m-1）x+2my+1=0与直线（m+3）x-（m-1）y+3=0相互垂直”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
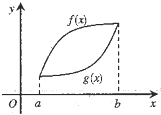已知函数f（x）和g（x）在区间[a，b]上的图象如图所示，那么下列说法正确的是（ ）| A、f（x）在a到b之间的平均变化率大于g（x）在a到b之间的平均变化率 |
| B、f（x）在a到b之间的平均变化率小于g（x）在a到b之间的平均变化率 |
| C、对于任意x0∈（a，b），函数f（x）在x=x0处的瞬时变化率总大于函数g（x）在x=x0处的瞬时变化率 |
| D、存在x0∈（a，b），使得函数f（x）在x=x0处的瞬时变化率小于函数g（x）在x=x0处的瞬时变化率 |
若函数f（x）=asinωx-cosωx的相邻两个零点的距离为π，且它的一条对称轴为x=
π，则f（-
）等于（ ）
| 2 |
| 3 |
| π |
| 3 |
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
已知函数y=tan（ωx）（ω＞0）的最小正周期为2π，则函数y=ωcosx的值域是（ ）
| A、[-2，2] | ||||
| B、[-1，1] | ||||
C、[-
| ||||
D、[-
|
设z=1-i（i是虚数单位），则
=（ ）
| 1 |
| z |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
