题目内容
过抛物线y2=2px(p>0)的焦点的直线交抛物线于A、B两点,若AB的中点为(1,-1),则抛物线的方程为( )
A、y2=(2+2
| ||
B、y2=4
| ||
C、y2=(1+2
| ||
| D、这样的抛物线不存在 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设A(x1,y1),B(x2,y2),由题设条件设出直线AB的方程,代入抛物线方程,由线段AB的中点的横纵坐标,推导出y1+y2=-2,由此能求出结果.
解答:
解:设A(x1,y1)、B(x2,y2)
∵AB中点为(1,-1),∴y1+y2=-2,(x1+x2)=2
∵直线过焦点(
,0),设AB方程为:x=ky+
,
代入抛物线方程可得y2=2p(ky+
),即y2-2pky-p2=0,
∴y1+y2=-2pk=-2,y1y2=-p2,
∴y12+y22=(y1+y2)2-2y1y2=4+2p2,
又y12+y22=2p(x1+x2)=2p×2=4p
∴4p=4+2p2,无解
∴这样的抛物线不存在,
故选:D
∵AB中点为(1,-1),∴y1+y2=-2,(x1+x2)=2
∵直线过焦点(
| p |
| 2 |
| p |
| 2 |
代入抛物线方程可得y2=2p(ky+
| p |
| 2 |
∴y1+y2=-2pk=-2,y1y2=-p2,
∴y12+y22=(y1+y2)2-2y1y2=4+2p2,
又y12+y22=2p(x1+x2)=2p×2=4p
∴4p=4+2p2,无解
∴这样的抛物线不存在,
故选:D
点评:本题考查抛物线的定义,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
已知f(x),g(x)对应值如下表,若f(g(a))≤a,则a的解集为( )
| x | 0 | 1 | -1 |
| f(x) | 1 | 0 | -1 |
| G(x) | -1 | 0 | 1 |
| A、{0,1} |
| B、{0,-1} |
| C、{1,-1} |
| D、{0,1,-1} |
已知
+
=1,(x>0,y>0),则x+y的最小值为( )
| 2 |
| x |
| 2 |
| y |
| A、1 | B、2 | C、4 | D、8 |
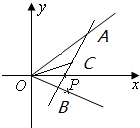 如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=
如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y= 在正方体ABCD-A1B1C1D1中,与AC平行,且过正方体三个顶点的截面是
在正方体ABCD-A1B1C1D1中,与AC平行,且过正方体三个顶点的截面是