题目内容
一条直线过点A(3,-2),且横截距与纵截距绝对值相等,求该直线的方程.
考点:直线的截距式方程
专题:直线与圆
分析:分类讨论:当直线l过原点时满足条件,即可得直线l的方程.当直线l的截距不为0时,可设直线l的方程为
+
=1.再利用已知可得
解得即可.
| x |
| a |
| y |
| b |
|
解答:
解:①当直线l过原点时满足条件,k=
,此时可得直线l的方程为:y=-
x.
②当直线l的截距不为0时,可设直线l的方程为
+
=1.
把点A(3,-2)代入可得:
+
=1.
又|a|=|b|,联立
解得
或
.
可知直线l的方程分别为:x+y=1,x-y=5.
综上可知:直线l的方程为:y=-
x,x+y=1,x-y=5.
| -2 |
| 3 |
| 2 |
| 3 |
②当直线l的截距不为0时,可设直线l的方程为
| x |
| a |
| y |
| b |
把点A(3,-2)代入可得:
| 3 |
| a |
| -2 |
| b |
又|a|=|b|,联立
|
|
|
可知直线l的方程分别为:x+y=1,x-y=5.
综上可知:直线l的方程为:y=-
| 2 |
| 3 |
点评:本题考查了直线的截距式方程、分类讨论思想方法,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
若f(x)=xex,则f′(1)=( )
| A、0 | B、e |
| C、2e | D、e2 |
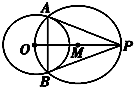 如图,已知P为⊙O外一点,以PO为直径作⊙M,⊙M交⊙O于A、B两点,求证:PA、PB是⊙O的切线.
如图,已知P为⊙O外一点,以PO为直径作⊙M,⊙M交⊙O于A、B两点,求证:PA、PB是⊙O的切线.