题目内容
已知双曲线C:
-
=1(a>0,b>0)的焦距为6,两顶点之间的距离为2,则C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、x2-
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据顶点坐标求得a,根据焦距求得c,进而根据b2=c2-a2求得b,进而求得双曲线的标准方程.
解答:
解:依题意可知a=1,c=3
∴b=2
根据顶点坐标可知焦点在x轴,
∴双曲线的方程为x2-
=1
故选:C.
∴b=2
| 2 |
根据顶点坐标可知焦点在x轴,
∴双曲线的方程为x2-
| y2 |
| 8 |
故选:C.
点评:本题主要考查了双曲线的标准方程.解题的关键是挖掘题设中的信息,充分利用a,b和c的关系,同时注意焦点是在x轴还是在y轴.

练习册系列答案
相关题目
已知a=(
)
,b=(
)
,c=(
)
,则a,b,c的大小关系是( )
| 3 |
| 5 |
| 1 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 3 |
| A、c<b<a |
| B、b<c<a |
| C、b<a<c |
| D、a<c<b |
已知b>0,则“ab2<b”是“ab<1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数f(x)=
的定义域为( )
| 1 |
| ln(x+1) |
| A、(-1,0)∪(0,+∞) |
| B、[-1,0)∪(0,+∞) |
| C、[-1,+∞) |
| D、(-1,+∞) |
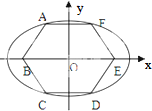 如图正六边形ABCDEF中,B、E为椭圆的焦点,A、C、D、F在椭圆上,则椭圆的离心率为( )
如图正六边形ABCDEF中,B、E为椭圆的焦点,A、C、D、F在椭圆上,则椭圆的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
M={x∈R|x≥2},a=π,则下列四个式子①a∈M;②{a}?M; ③a⊆M;④{a}∩M=π,其中正确的是( )
| A、①② | B、①④ | C、②③ | D、①②④ |
已知实数x>y,且y≠0,则下列结论正确的是( )
A、
| ||||
| B、cx>cy(c∈R) | ||||
| C、x3>y3 | ||||
D、
|
在等差数列{an}中,已知a1=
,a4+a5=
,若an=33,则n=( )
| 1 |
| 3 |
| 16 |
| 3 |
| A、50 | B、49 | C、48 | D、47 |