题目内容
分别写出下列命题的逆命题、逆否命题,并判断它们的真假:
(1)若q<1,则方程x2+2x+q=0有实根;
(2)若x2+y2=0,则x,y全为零.
(1)若q<1,则方程x2+2x+q=0有实根;
(2)若x2+y2=0,则x,y全为零.
考点:四种命题
专题:简易逻辑
分析:首先根据逆命题、逆否命题两种命题的基本概念,分别写出两个命题的逆命题、逆否命题;然后根据等价命题的原理和规律,判断这两种命题的真假即可.
解答:
解:(1)原命题:若q<1,则方程x2+2x+q=0有实根;
逆命题:若方程x2+2x+q=0有实根,则q<1,它是一个假命题,
因为q=1时,方程x2+2x+q=0有实根x=-1;
逆否命题:若方程x2+2x+q=0无实根,则q≥1,它是一个真命题.
(2)原命题:若x2+y2=0,则x,y全为零;
逆命题:若x、y全为零,则x2+y2=0,它是一个真命题;
逆否命题:若x、y不全为零,则x2+y2≠0,它是一个真命题.
逆命题:若方程x2+2x+q=0有实根,则q<1,它是一个假命题,
因为q=1时,方程x2+2x+q=0有实根x=-1;
逆否命题:若方程x2+2x+q=0无实根,则q≥1,它是一个真命题.
(2)原命题:若x2+y2=0,则x,y全为零;
逆命题:若x、y全为零,则x2+y2=0,它是一个真命题;
逆否命题:若x、y不全为零,则x2+y2≠0,它是一个真命题.
点评:本题主要考查了四种命题的含义及其运用,属于基础题,解答此题的关键是等价命题的原理和规律的运用.

练习册系列答案
相关题目
已知双曲线C:
-
=1(a>0,b>0)的焦距为6,两顶点之间的距离为2,则C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、x2-
| ||||
D、
|
等差数列{an},a7-2a4=-1,且a3=0,则公差d=( )
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
直线y=x+
被曲线y=
x2截得线段的中点到原点的距离为( )
| 3 |
| 2 |
| 1 |
| 2 |
| A、29 | ||||
B、
| ||||
C、
| ||||
D、
|
 如图,△ABC的AB边长为2,P,Q分别是AC,BC中点,记
如图,△ABC的AB边长为2,P,Q分别是AC,BC中点,记| AB |
| AP |
| BA |
| BQ |
| AB |
| AQ |
| BA |
| BP |
| A、m=2,n=4 |
| B、m=3,n=1 |
| C、m=2,n=6 |
| D、m=3n,但m,n的值不确定 |
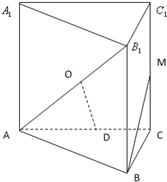 已知直三棱柱ABC-A1B1C1的底面△ABC中,∠C=90°,BC=
已知直三棱柱ABC-A1B1C1的底面△ABC中,∠C=90°,BC=