题目内容
13.函数f(x)=$\frac{x-{x}^{3}}{(1+{x}^{2})^{2}}$的值域为[-$\frac{1}{4}$,$\frac{1}{4}$].分析 求导f′(x)=$\frac{(1-3{x}^{2})({x}^{2}+1)^{2}-(x-{x}^{3})2({x}^{2}+1)2x}{({x}^{2}+1)^{4}}$,从而确定函数的驻点,从而求函数的值域.
解答 解:∵f(x)=$\frac{x-{x}^{3}}{(1+{x}^{2})^{2}}$,
∴f′(x)=$\frac{(1-3{x}^{2})({x}^{2}+1)^{2}-(x-{x}^{3})2({x}^{2}+1)2x}{({x}^{2}+1)^{4}}$,
令f′(x)=0得(3x2-1)(x2+1)2-(x3-x)•2•(x2+1)•2x=0,
∴(3x2-1)(x2+1)-4x2(x2-1)=0,
整理可得x4-6x2+1=0,
解得x1=1+$\sqrt{2}$,x2=$\sqrt{2}$-1,x3=-1-$\sqrt{2}$,x4=1-$\sqrt{2}$,
∴f(x1)=-$\frac{1}{4}$,f(x2)=$\frac{1}{4}$,f(x3)=$\frac{1}{4}$,f(x4)=-$\frac{1}{4}$,
∴函数f(x)=$\frac{x-{x}^{3}}{(1+{x}^{2})^{2}}$的值域为[-$\frac{1}{4}$,$\frac{1}{4}$];
故答案为:[-$\frac{1}{4}$,$\frac{1}{4}$].
点评 本题考查了导数的综合应用.

练习册系列答案
相关题目
2.下列变量是线性相关的是( )
| A. | 人的身高与视力 | B. | 角的大小与弧长 | ||
| C. | 收入水平与消费水平 | D. | 人的年龄与身高 |
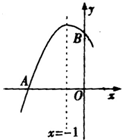 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论: