题目内容
已知函数f(x)=sin(2x+φ)在区间[
,
]上单调递减,则实数φ的取值可以是( )
| π |
| 3 |
| 5π |
| 6 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:根据三角函数的单调性的性质,进行求解即可.
解答:
解:∵
≤x≤
,
∴
≤2x≤
,
则
+φ≤2x+φ≤
+φ,
若φ=-
,则
≤2x+φ≤
,此时函数f(x)单调递减,满足条件.
若φ=
,则
≤2x+φ≤
,此时函数f(x)不单调递减,不满足条件.
若φ=
,则
≤2x+φ≤
,此时函数f(x)不单调递减,不满足条件.
若φ=
,则π≤2x+φ≤2π,此时函数f(x)不单调递减,不满足条件.
故选:A
| π |
| 3 |
| 5π |
| 6 |
∴
| 2π |
| 3 |
| 5π |
| 3 |
则
| 2π |
| 3 |
| 5π |
| 3 |
若φ=-
| π |
| 6 |
| π |
| 2 |
| 3π |
| 2 |
若φ=
| π |
| 6 |
| 5π |
| 6 |
| 11π |
| 6 |
若φ=
| π |
| 4 |
| 11π |
| 12 |
| 7π |
| 4 |
若φ=
| π |
| 3 |
故选:A
点评:本题主要考查三角函数的单调性的求解决,结合正弦函数的图象和性质是解决本题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
已知平面向量
=(1,2),
=(x,1),如果向量
+2
与2
-
平行,那么
•(
-
)等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、-2 | ||
| B、-1 | ||
C、
| ||
D、
|
直线l1:ax+(1-a)y=0,l2:(a-1)x+3y=2互相垂直,则a的值为( )
| A、-3 | B、1 |
| C、1或-3 | D、1或3 |
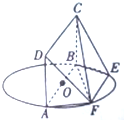 如图,AB为圆O的直径,四边形ABCD为正方形,点E、F在圆O上,AD⊥AF,AB=4,EF=AF=2
如图,AB为圆O的直径,四边形ABCD为正方形,点E、F在圆O上,AD⊥AF,AB=4,EF=AF=2