题目内容
若ab≠0,则ax-y+b=0和bx2+ay2=ab所表示的曲线只可能是图中的( )
A、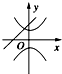 |
B、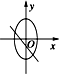 |
C、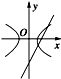 |
D、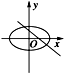 |
考点:直线与圆锥曲线的关系
专题:圆锥曲线中的最值与范围问题
分析:方程可化为y=ax+b和
+
=1.由此利用直线和椭圆的性质利用排除法求解.
| x2 |
| a |
| y2 |
| b |
解答:
解:方程可化为y=ax+b和
+
=1.
从B,D中的两椭圆看a,b∈(0,+∞),
但B中直线有a<0,b<0矛盾,应排除;
D中直线有a<0,b>0矛盾,应排除;
再看A中双曲线的a<0,b>0,但直线有a>0,b>0,也矛盾,应排除;
C中双曲线的a>0,b<0和直线中a,b一致.
故选:C.
| x2 |
| a |
| y2 |
| b |
从B,D中的两椭圆看a,b∈(0,+∞),
但B中直线有a<0,b<0矛盾,应排除;
D中直线有a<0,b>0矛盾,应排除;
再看A中双曲线的a<0,b>0,但直线有a>0,b>0,也矛盾,应排除;
C中双曲线的a>0,b<0和直线中a,b一致.
故选:C.
点评:本题考查直线与椭圆的图象的判断,是中档题,解题时要认真审题,注意直线与椭圆的性质的合理运用.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
已知A,B在抛物线y2=2px(p>0)上,O为坐标原点,如果|OA|=|OB|且△AOB的重心恰好是此抛物线的焦点F,则AB直线的方程是( )
| A、x-p=0 |
| B、4x-3p=0 |
| C、2x-5p=0 |
| D、2x-5p=0 |
以双曲线
-
=1的左顶点为焦点的抛物线的标准方程是( )
| x2 |
| 4 |
| y2 |
| 9 |
| A、y2=4x |
| B、y2=16x |
| C、y2=8x |
| D、y2=-8x |
已知y=x-
(k≠0),若f′(1)=
则k等于( )
| k |
| x |
| 1 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
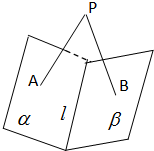 如图,p是二面角α-l-β内的一点(p∉α,p∉β),PA⊥α于点A,PB⊥β于点B,∠APB=35°,则二面角α-l-β的大小是
如图,p是二面角α-l-β内的一点(p∉α,p∉β),PA⊥α于点A,PB⊥β于点B,∠APB=35°,则二面角α-l-β的大小是