题目内容
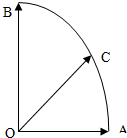如图，| OA |
| OB |
| OA |
| OB |
| OA |
| OC |
| OA |
| OB |
考点：平面向量的基本定理及其意义
专题：计算题,作图题,平面向量及应用
分析：由题意作图如下，可知x+y=cosa+sina（0≤a≤
），从而可得其取值范围．
| π |
| 2 |
解答：
解：如下图：
=x
+y
=cosa
+sina
，
则x+y=cosa+sina（0≤a≤
），
故答案为[1，
]．
| OC |
| OA |
| OB |
| OA |
| OB |
则x+y=cosa+sina（0≤a≤
| π |
| 2 |
故答案为[1，
| 2 |
点评：本题考查了平面向量的基本定理及其几何意义，属于基础题．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
已知集合A={x||2x-1|＜3}，B={x|
＜0}，则A∩B=（ ）
| 2x+1 |
| 3-x |
A、（-1，
| ||
| B、（2，3） | ||
C、（-
| ||
D、（-1，
|
用反证法证明“a，b∈N*，ab可被5整除，那么a，b中至少有一个能被5整除”时，假设的内容是（ ）
| A、a不能被5整除 |
| B、b不能被5整除 |
| C、a，b都不能被5整除 |
| D、以上都不正确 |
设y=lnx-8x2，则此函数在区间（
，
）和（（1，+∞）内分别（ ）
| 1 |
| 4 |
| 1 |
| 2 |
| A、单调递增，单调递减 |
| B、单调递增，单调递增 |
| C、单调递减，单调递增 |
| D、单调递减，单调递减 |