题目内容
设集合A={m-2，-3}，b={2m-1，m-3}，若A∩B={-3}，则m的值为 ．
考点：交集及其运算
专题：集合
分析：由A∩B={-3}，得2m-1=-3或m-3=-3，求解m的值后代回原集合验证元素的特性后得答案．
解答：
解：集合A={m-2，-3}，B={2m-1，m-3}，
由A∩B={-3}，得
2m-1=-3或m-3=-3．
解得m=-1或m=0．
当m=-1时，集合A违背集合中元素的互异性．
当m=0时，A={-2，-3}，B={-1，-3}．符合题意．
故m=0．
故答案为：0．
由A∩B={-3}，得
2m-1=-3或m-3=-3．
解得m=-1或m=0．
当m=-1时，集合A违背集合中元素的互异性．
当m=0时，A={-2，-3}，B={-1，-3}．符合题意．
故m=0．
故答案为：0．
点评：本题考查了交集及其运算，考查了集合中元素的特性，是基础题．
练习册系列答案
相关题目
如图，设数列{xn}满足log2xn+1=1+log2xn（n∈N+），且x1+x2+…+x10=10，记{xn}的前n项和为Sn，则S20=（ ）
| A、1 025 |
| B、1 024 |
| C、10 250 |
| D、10 240 |
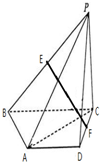已知在四棱锥P-ABCD中，PD⊥面ABCD，AD∥BC，CD=13，AB=12，BC=10，AD=