题目内容
17.已知命题$p:?n∈N,{2^n}>\sqrt{n}$,则¬p是( )| A. | $?n∈N,{2^n}≤\sqrt{n}$ | B. | $?n∈N,{2^n}<\sqrt{n}$ | C. | $?n∈N,{2^n}≤\sqrt{n}$ | D. | $?n∈N,{2^n}>\sqrt{n}$ |
分析 利用全称命题的否定是特称命题,可以求出¬p.
解答 解:因为命题p是全称命题,所以利用全称命题的否定是特称命题可得:
¬p.$?n∈N,{2^n}≤\sqrt{n}$
故选:C
点评 本题主要考查了含有量词的命题的否定,要求掌握含有量词的命题的否定的两种形式,全称命题的否定是特称命题,特称命题的否定是全称命题.

练习册系列答案
相关题目
8.等差数列{an}的前n项和为Sn,且S5=15,a2=5,则公差d等于( )
| A. | -3 | B. | -2 | C. | -1 | D. | 2 |
5.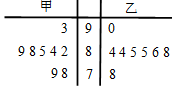 某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )
某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )
 某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )
某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )| A. | 甲、乙生产的零件尺寸的中位数相等 | |
| B. | 甲、乙生产的零件质量相当 | |
| C. | 甲生产的零件质量比乙生产的零件质量好 | |
| D. | 乙生产的零件质量比甲生产的零件质量好 |
7.已知F1,F2为双曲线E的左,右焦点,点M在E的渐近线上,△F1F2M为等腰三角形,且顶角为120°,则E的离心率为( )
| A. | $\frac{\sqrt{7}}{2}$ | B. | 2 | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{5}$ |
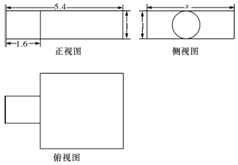 中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器----商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中的x为3.
中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器----商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中的x为3.