题目内容
12.如图1,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起,得到如图2所示的四棱锥D1-ABCE,其中平面D1AE⊥平面ABCE.(Ⅰ)证明:BE⊥平面D1AE;
(Ⅱ)求三棱锥C-BD1E的体积.
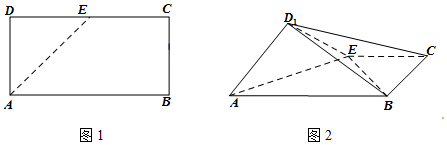
分析 (Ⅰ)过D1作D1F⊥AE交AE于F,由已知结合面面垂直的性质可得D1F⊥平面ABCE,进一步得到BE⊥D1F,在△ABE中,$AB=4,AE=BE=2\sqrt{2}$,满足AB2=AE2+BE2 ,可得BE⊥AE,再由线面垂直的判定可得BE⊥平面D1AE;
(Ⅱ)由(Ⅰ)可得${D_1}F=\sqrt{2}$,且为三棱锥D1-BCE的高,然后利用等积法求得三棱锥C-BD1E的体积.
解答 (Ⅰ)证明:过D1作D1F⊥AE交AE于F,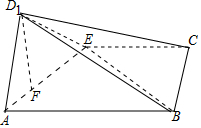
∵平面D1AE⊥平面ABCE,且平面D1AE∩平面ABCE=AE,∴D1F⊥平面ABCE,
∵BE?平面ABCE,∴BE⊥D1F,
在△ABE中,$AB=4,AE=BE=2\sqrt{2}$,满足AB2=AE2+BE2 ,
∴BE⊥AE,又∵AE∩D1F=F,
∴BE⊥平面D1AE;
(Ⅱ)解:由(Ⅰ)可得${D_1}F=\sqrt{2}$,且为三棱锥D1-BCE的高,
由此可得${V_{C-B{D_1}E}}={V_{{D_1}-BCE}}=\frac{1}{3}{S_{△BCE}}•{D_1}F=\frac{1}{3}×\frac{1}{2}×BC×CE×{D_1}F=\frac{1}{6}×2×2×\sqrt{2}=\frac{{2\sqrt{2}}}{3}$.
点评 本题考查直线与平面垂直的判定和性质,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
相关题目
2.复数(2+i)i的共轭复数的虚部是( )
| A. | 2 | B. | -2 | C. | 2i | D. | -2i |
17.已知命题$p:?n∈N,{2^n}>\sqrt{n}$,则¬p是( )
| A. | $?n∈N,{2^n}≤\sqrt{n}$ | B. | $?n∈N,{2^n}<\sqrt{n}$ | C. | $?n∈N,{2^n}≤\sqrt{n}$ | D. | $?n∈N,{2^n}>\sqrt{n}$ |