题目内容
2．在${（{x^2}+\frac{2}{x^3}）^5}$的展开式中，常数项为40．（用数字作答）．分析 在${（{x^2}+\frac{2}{x^3}）^5}$展开式的通项公式中，令x的幂指数等于零，求出r的值，即可求出展开式的常数项．
解答 解：由于${（{x^2}+\frac{2}{x^3}）^5}$展开式的通项公式为Tr+1=${C}_{5}^{r}$•2r•x10-5r，
令10-5r=0，解得r=2，故展开式的常数项是40，
故答案为40．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，属于中档题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
10．已知函数f（x）=lnx，曲线y=g（x）与曲线y=f（x）关于直线y=x对称，若存在一条过原点的直线与曲线y=f（x）和曲线y=g（ax）都相切，则实数a的值为$\frac{1}{e^2}$．
17．已知命题$p：?n∈N，{2^n}＞\sqrt{n}$，则￢p是（ ）
| A． | $?n∈N，{2^n}≤\sqrt{n}$ | B． | $?n∈N，{2^n}＜\sqrt{n}$ | C． | $?n∈N，{2^n}≤\sqrt{n}$ | D． | $?n∈N，{2^n}＞\sqrt{n}$ |
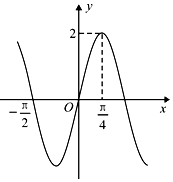已知函数f（x）=Asin（ωx）（ω＞0）的图象如图所示．