题目内容
正方形ABCD的顶点A,C在抛物线y2=4x上,一条对角线BD在直线y=-
x+2上.
(Ⅰ)求AC所在的直线方程;
(Ⅱ)求正方形ABCD的面积.
| 1 |
| 2 |
(Ⅰ)求AC所在的直线方程;
(Ⅱ)求正方形ABCD的面积.
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据正方形的性质可知AC⊥BD,进而可知AC斜率是2,设直线AC方程为y=2x+b,代入抛物线方程,根据韦达定理表示出x1+x2和x1x2,进而求得y1+y2,则AC的中点坐标可得,代入直线x+2y-4=0中求得b,进而求得AC所在的直线方程;
(Ⅱ)求出x1+x2和x1x2的值,求得(x1-x2)2和(y1-y2)2,从而求得AC的长度,即可求正方形ABCD的面积.
(Ⅱ)求出x1+x2和x1x2的值,求得(x1-x2)2和(y1-y2)2,从而求得AC的长度,即可求正方形ABCD的面积.
解答:
解:(Ⅰ)由题意可知:AC⊥BD.
设AC所在的直线方程为y=2x+b,
代入抛物线方程得4x2+4bx+b2=4x,即4x2+(4b-4)x+b2=0
设A(x1,y1),C(x2,y2),
∴x1+x2=1-b,
∵y=2x+b,
∴y1+y2=2x1+b+2x2+b=2(1-b)+2b=2,
∵AC中点(
,1)在BD上,
∴1=-
•
+2,
∴b=-3,
∴AC所在的直线方程为2x-y-3=0;
(Ⅱ)由(Ⅰ)知4x2-16x+9=0,
∴x1+x2=4,x1x2=
,
∴(x1-x2)2=(x1+x2)2-4x1x2=7,
(y1-y2)2=[2(x1-x2)]2=28,
∴AC=
=
,
∴正方形ABCD的面积为
×35=
.
设AC所在的直线方程为y=2x+b,
代入抛物线方程得4x2+4bx+b2=4x,即4x2+(4b-4)x+b2=0
设A(x1,y1),C(x2,y2),
∴x1+x2=1-b,
∵y=2x+b,
∴y1+y2=2x1+b+2x2+b=2(1-b)+2b=2,
∵AC中点(
| 1-b |
| 2 |
∴1=-
| 1 |
| 2 |
| 1-b |
| 2 |
∴b=-3,
∴AC所在的直线方程为2x-y-3=0;
(Ⅱ)由(Ⅰ)知4x2-16x+9=0,
∴x1+x2=4,x1x2=
| 9 |
| 4 |
∴(x1-x2)2=(x1+x2)2-4x1x2=7,
(y1-y2)2=[2(x1-x2)]2=28,
∴AC=
| 7+28 |
| 35 |
∴正方形ABCD的面积为
| 1 |
| 2 |
| 35 |
| 2 |
点评:本题主要考查了直线与圆锥曲线的综合问题.弦长问题、最值问题、对称问题等考查了学生综合分析问题的能力.

练习册系列答案
相关题目
 已知椭圆
已知椭圆 如图,底面为正方形的四棱锥S-ABCD 中,P为侧棱SD上的点且SD⊥平面PAC,每条侧棱的长都是底面边长的
如图,底面为正方形的四棱锥S-ABCD 中,P为侧棱SD上的点且SD⊥平面PAC,每条侧棱的长都是底面边长的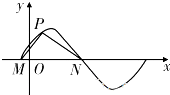 如图所示,M,N是函数y=2sin(ωx+φ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时
如图所示,M,N是函数y=2sin(ωx+φ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时