题目内容
在△ABC中，内角A，B，C的对边分别为a，b，c，若A=60°a=2，b=
，则边c的长为 ．
2
| ||
| 3 |
考点：正弦定理,余弦定理
专题：解三角形
分析：利用余弦定理：a2=b2+c2-2cbcosA，代入即可解出．
解答：
解：由余弦定理可得：a2=b2+c2-2cbcosA，
∴22=(
)2+c2-
ccos60°，
化为3c2-2
c-8=0，
∵c＞0，解得c=
．
故答案为：
．
∴22=(
2
| ||
| 3 |
4
| ||
| 3 |
化为3c2-2
| 3 |
∵c＞0，解得c=
| 4 |
| 3 |
| 3 |
故答案为：
| 4 |
| 3 |
| 3 |
点评：本题考查了余弦定理的应用，属于基础题．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
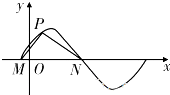如图所示，M，N是函数y=2sin（ωx+φ）（ω＞0）图象与x轴的交点，点P在M，N之间的图象上运动，当△MPN面积最大时
