题目内容
 如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,并且底面是正三角形,如果圆柱的体积是16π,底面直径与母线长相等.
如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,并且底面是正三角形,如果圆柱的体积是16π,底面直径与母线长相等.(1)求正三角形ABC边长;
(2)三棱柱的体积V是多少?
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:(1)求得棱柱的底面是正三角形,其外接圆半径为r=2,即可求正三角形ABC边长;
(2)利用三棱柱的体积公式,可求三棱柱的体积V.
(2)利用三棱柱的体积公式,可求三棱柱的体积V.
解答:
解:(1)设圆柱的底面半径为r,
则由已知得圆柱的母线长及三棱柱的高为2r.…(2分)
由πr22r=16π,得r=2,则三棱柱的高为4.…(4分)
∵三棱柱的底面是正三角形,其外接圆半径为r=2
∴边长AB=
×3=2
,…(8分)
(2)∵S△ABC=
×AB2=3
∴三棱柱的体积V=S△ABC•AA1=3
×4=12
…(12分)
则由已知得圆柱的母线长及三棱柱的高为2r.…(2分)
由πr22r=16π,得r=2,则三棱柱的高为4.…(4分)
∵三棱柱的底面是正三角形,其外接圆半径为r=2
∴边长AB=
| 2 | ||
|
| 3 |
(2)∵S△ABC=
| ||
| 4 |
| 3 |
∴三棱柱的体积V=S△ABC•AA1=3
| 3 |
| 3 |
点评:本题考查圆柱的体积公式与三棱柱的体积公式的应用,考查计算能力,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
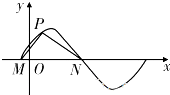 如图所示,M,N是函数y=2sin(ωx+φ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时
如图所示,M,N是函数y=2sin(ωx+φ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时