题目内容
已知
=(
,-1),
=(
,
).
(1)设
与
的夹角为θ,解关于x的不等式:log3(2x-1)≤21-sinθ
(2)若存在不同时为0的实数k和t,使
=a+(t-3)b,
=-ka+tb,且
⊥
,试求函数关系式k=f(t);
(3)求函数k=f(t)的最小值.
| a |
| 3 |
| b |
| 1 |
| 2 |
| ||
| 2 |
(1)设
| a |
| b |
(2)若存在不同时为0的实数k和t,使
| x |
| y |
| x |
| y |
(3)求函数k=f(t)的最小值.
考点:三角函数中的恒等变换应用
专题:函数的性质及应用
分析:(1)利用向量的数量积的坐标运算可求得θ=
,从而可解log3(2x-1)≤1,即得其解集;
(2)依题意,由
⊥
,得-ka2+t(t-3)b2=0,于是可求得k;
(3)由(2)知k=
t(t-3),配方后,利用二次函数的性质即可求得函数k=f(t)的最小值.
| π |
| 2 |
(2)依题意,由
| x |
| y |
(3)由(2)知k=
| 1 |
| 4 |
解答:
解:(1)由
•
=
-
=0,得
⊥
.
∵
与
的夹角为θ,
∴θ=
,∴log3(2x-1)≤21-1=1,
∴2x-1≤3,
解得:0<x≤2,即原不等式的解集为{x|0<x≤2}…(4分)
(2)由
⊥
,得,
•
=[a+(t-3)b]•(-ka+tb)=0,即-ka2-k(t-3)a•b+ta•b+t(t-3)b2=0.
-ka2+t(t-3)b2=0.
∴k=
t(t-3).…(9分)
(3)k=
t(t-3)=
(t-
)2-
,
所以当t=
时,k取最小值-
.…(13分)
| a |
| b |
| ||
| 2 |
| ||
| 2 |
| a |
| b |
∵
| a |
| b |
∴θ=
| π |
| 2 |
∴2x-1≤3,
解得:0<x≤2,即原不等式的解集为{x|0<x≤2}…(4分)
(2)由
| x |
| y |
| x |
| y |
-ka2+t(t-3)b2=0.
∴k=
| 1 |
| 4 |
(3)k=
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| 9 |
| 16 |
所以当t=
| 3 |
| 2 |
| 9 |
| 16 |
点评:本题考查利用向量的数量积的坐标运算,突出考查对数函数的性质与二次函数的最值,考查等价转化思想与运算求解能力,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目

 已知椭圆
已知椭圆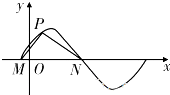 如图所示,M,N是函数y=2sin(ωx+φ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时
如图所示,M,N是函数y=2sin(ωx+φ)(ω>0)图象与x轴的交点,点P在M,N之间的图象上运动,当△MPN面积最大时