题目内容
6.已知命题:“若曲线$\frac{x^2}{m}+\frac{y^2}{n}=1$为椭圆,则mn>0”则原命题、逆命题、否命题、逆否命题这四个命题中,真命题的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 根据四种命题真假之间的关系进行判断即可.
解答 解:若曲线$\frac{x^2}{m}+\frac{y^2}{n}=1$为椭圆,则m,n>0且m≠n,则mn>0成立,即原命题为真命题,则逆否命题也为真命题.
逆命题为若mn>0,曲线$\frac{x^2}{m}+\frac{y^2}{n}=1$为椭圆,也为假命题,当m=n=1时,满足mn>0,但曲线$\frac{x^2}{m}+\frac{y^2}{n}=1$表示圆不是椭圆,
故逆命题为假命题.,则否命题也为假命题,
故四个命题中真命题的个数为2个,
故选:C
点评 本题主要考查四种命题的真假判断,根据逆否命题的真假性相同只需要判断原命题和逆命题的真假即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.二次曲线$\left\{\begin{array}{l}{x=4cosθ}\\{y=3sinθ}\end{array}\right.$(θ为参数)的焦点坐标为( )
| A. | (±5,0) | B. | (0,5) | C. | (±$\sqrt{7}$,0) | D. | (0,±$\sqrt{7}$) |
11.函数$y={x^2}+\frac{1}{x}+1$在x=1处的切线方程是( )
| A. | x-y+2=0 | B. | x-y-4=0 | C. | x+y-4=0 | D. | x+y+2=0 |
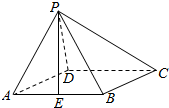 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.